Extending Upward Planar Graph Drawings
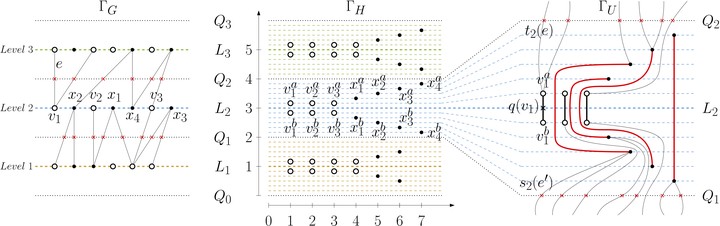 The UPE-FUE problem is NP-complete. (Left) An instance $(G,\ell,\prec)$ of Partial Level Planarity with a prescribed upward embedding. (Center and right) An instance $(U,H,\Gamma_H)$ of UPE-FUE equivalent to $(G,\ell,\prec)$.
The UPE-FUE problem is NP-complete. (Left) An instance $(G,\ell,\prec)$ of Partial Level Planarity with a prescribed upward embedding. (Center and right) An instance $(U,H,\Gamma_H)$ of UPE-FUE equivalent to $(G,\ell,\prec)$.
Abstract
In this paper we study the computational complexity of the Upward Planarity Extension problem, which takes in input an upward planar drawing $\Gamma_H$ of a subgraph $H$ of a directed graph $G$ and asks whether $\Gamma_H$ can be extended to an upward planar drawing of $G$. Our study fits into the line of research on the extensibility of partial representations, which has recently become a mainstream in Graph Drawing.
We show the following results.
- First, we prove that the Upward Planarity Extension problem is NP-complete, even if $G$ has a prescribed upward embedding, the vertex set of $H$ coincides with the one of $G$, and $H$ contains no edge.
- Second, we show that the Upward Planarity Extension problem can be solved in $O(n \log n)$ time if $G$ is an $n$-vertex upward planar $st$-graph. This result improves upon a known $O(n^2)$-time algorithm, which however applies to all $n$-vertex single-source upward planar graphs.
- Finally, we show how to solve in polynomial time a surprisingly difficult version of the Upward Planarity Extension problem, in which $G$ is a directed path or cycle with a prescribed upward embedding, $H$ contains no edges, and no two vertices share the same $y$-coordinate in $\Gamma_H$.
Type
Publication
In 16th International Symposium on Algorithms and Data Structures (WADS 2019)