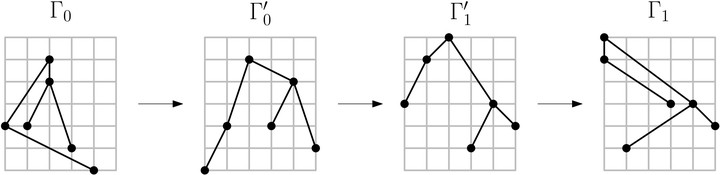
 A 3-step morph between two order-preserving strictly-upward straight-line planar grid drawings of a tree.
A 3-step morph between two order-preserving strictly-upward straight-line planar grid drawings of a tree.
Abstract
In this paper, we study planar morphs between straight-line planar grid drawings of trees. A morph consists of a sequence of morphing steps, where in a morphing step vertices move along straight-line trajectories at constant speed. We show how to construct planar morphs that simultaneously achieve a reduced number of morphing steps and a polynomially-bounded resolution. We assume that both the initial and final drawings lie on the grid and we ensure that each morphing step produces a grid drawing; further, we consider both upward drawings of rooted trees and drawings of arbitrary trees.
Type
Publication
In 16th International Symposium on Algorithms and Data Structures (WADS 2019)