Giordano Da Lozzo
Assistant Professor (RTDb)
Roma Tre University
Giordano Da Lozzo is a tenure-track assistant professor (RTDb) at Roma Tre University, working in the research group on Graph Algorithms and Network Visualization. Prior to this position, he was a research associate (RTDa) for three years and a postdoctoral researcher (assegnista di ricerca) for four years at the same institution, mentored by Giuseppe Di Battista, and an assistant project scientist for one year, between 2016 and 2017, in the Theory Group of the Center for Algorithms and Theory of Computation at University of California, Irvine, jointly mentored by Michael T. Goodrich and David A. Eppstein.
He obtained his PhD degree in Computer Science and Automation Engineering in 2015 from Roma Tre University, jointly advised by Giuseppe Di Battista and Maurizio Patrignani, where he also graduated cum laude in Computer Engineering presenting a thesis that received the AICA-Confindustria award as best thesis in Information Communication Technology. He was a Leonardo da Vinci fellow at the RIPE Network Coordination Center in Amsterdam and a visiting scholar at the Charles University in Prague. He was also a research visitor at the Universität Tübingen, the Technische Universiteit Eindhoven, and the Karlsruhe Institute of Technology. His Erdös Number is 2.
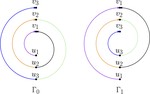
His research interests are in algorithm engineering and complexity, focused in particular on the practical and theoretical challenges arising from the design of efficient algorithms for the analysis and visualization of networks. His primary area of research lies in graph drawing, a research field at the intersection of the areas of computational geometry, combinatorial optimization, discrete mathematics, and graph theory. He is involved in several research projects exploring fundamental questions about the visualization of large and evolving networks, visualizations for cybersecurity, layouts of simultaneous and clustered networks, as well as contact and hybrid representations of real-world graphs.
He has published 29 articles in prestigious journals in the field of algorithms, such as ACM Transactions on Algorithms, Algorithmica, Discrete and Computational Geometry, SIAM Journal on Computing, and Theoretical Computer Science. He has published 48 conference papers in selective international venues, such as the Symposium on Data Structures and Algorithms (SODA), the Symposium on Computational Geometry (SoCG), the International Colloquium on Automata, Languages and Programming (ICALP), and the European Symposium on Algorithms (ESA). Moreover, he is the coauthor of a book chapter entitled Beyond Clustered Graphs. Finally, he has served as a program committee member in internal conferences and as a reviewer for several journals and research funding projects.
Interests
- Graph Drawing
- Graph Theory
- Discrete & Computational Geometry
- Algorithms and Data Structures
PhD Students
-
current
Education
-
Associate Professor Habilitation (09/H1 - Information Processing Systems), from 2022 to 2031
The Italian Ministry of Education, Universities and Research (MIUR)
-
PhD in Computer Science and Automation Engineering, 2015
Roma Tre University
-
MEng in Computer Science (110/110 cum laude), 2010
Roma Tre University