SEFE = C-Planarity?

Abstract

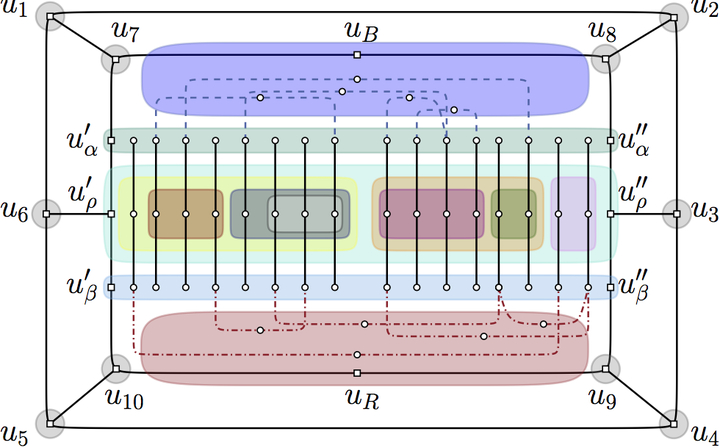
In this article, we deepen the understanding of the connection between two long-standing graph drawing open problems, Simultaneous Embedding with Fixed Edges (SEFE-2) and Clustered Planarity (C-Planarity). Given two planar graphs on the same set of vertices, the SEFE-2 problem asks to find planar drawings of the two graphs such that each vertex lies on the same point and each common edge is represented by the same curve in both drawings. Given a planar graph together with a recursive clustering of its vertices, the C-Planarity problem asks to find a planar drawing of the graph and a representation of each cluster as a simple region enclosing all and only the vertices of the cluster such that no unnecessary intersection involving clusters and edges is created. In a recent article at GD’12, Marcus Schaefer presented a reduction from C-Planarity to SEFE-2. We prove that a reduction exists also in the opposite direction, if we restrict to instances of SEFE-2 in which the graph induced by the common edges is connected. We pose as an intriguing open question whether the two problems are polynomial-time equivalent.