Algoritmi a chiave pubblica
Buona parte dei sistemi crittografici oggi in uso ricorre ad algoritmi simmetrici cioè quelli dove la chiave segreta è condivisa da due soli enti. Questo permette loro l' utilizzo di un canale protetto in entrambe le direzioni. Esistono tuttavia algoritmi asimmetrici, più comunemente conosciuti come a chiave pubblica.
Tale denominazione deriva dal fatto che una delle due chiavi (quella del mittente) è resa pubblica mentre quella del ricevente è mantenuta segreta. Questi algoritmi come è facile notare sono unidizezionali, cioè la protezione è assicurata in un solo senso. Per poter comunicare nel verso opposto è necessario disporre di una ulteriore coppia di chiavi.
Il vantaggio di tale algoritmo è quello di eliminare il problema del trasporto della chiave segreta da un ente all' altro.

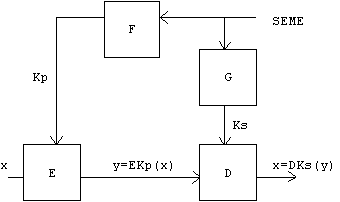
La figura posta qui sopra facilita la comprensione del principio di funzionamento dell' algoritmo a chiave pubblica.
Il messaggio "x" viene codificato attraverso l' algoritmo E e la chiave pubblica Kp. Si invia quindi al destinatario il messaggio cifrato "y". La decodifica avviene attraverso l' algoritmo D e la chiave segreta Ks.
Affinchè il processo D sia l' inverso di E occorre che le due chiavi siano correlate tra loro. Gli algoritmi F e G hanno la funzione di generare le chiavi a partire da un valore casuale (SEME) prelevato da un grande insieme di valori possibili .
Sono di dominio pubblico gli algoritmi di codifica (E) , di decodifica (D) e l' algoritmo F che genera la chiave pubblica Kp.
Il destinatario attraverso la sua chiave segreta Ks è in grado di ricostruire il testo chiaro. Sorge il problema però di risalire al mittente, cioè uno schema così semplificativo non prevede una forma di autenticazione di chi invia il messaggio perchè i possibili mittenti sono tutti coloro che posseggono una chiave Kp!
Per cui se nei sistemi asimmetrici è stato evitato il trasporto della chiave segreta, in compenso si ha il problema di garantire al mittente che la chiave da lui utilizzata sia autentica.
Un nemico infatti potrebbe intromettersi trasmettendo al mittente un falsa chiave pubblica. Tutti i messaggi che questo invia verrebbero intercettati dall' intruso, che li decodifica per se e li ricodifica con la Kp esatta per il destinatario che non si accorgerebbe di nulla.
Solo il ritardo dovuto all' intromissione potrebbe svelare l' inganno.
Per tale motivo la realizzazione di un algoritmo a chiave pubblica non risulta così semplice. Essendo noti Kp e l'algoritmo di codifica E deve risultare impossibile a chiunque (escluso il ricevente) risalire al testo chiaro "x" partendo da quello cifrato "y". Funzioni di questo tipo si dicono funzioni unidirezionali .
Anche l' algoritmo F deve avere tale proprietà, poichè sarà possibile risalire al seme partendo da Kp, e quindi calcolare Ks che dovrebbe rimanere segreta.
L' algoritmo D deve possedere le caratteristiche di un algoritmo di decodifica, ossia rendere impossibile il calcolo di Kp avendo parte del testo decifrato.
Al fine di risolvere questo problema si ricorre ad una classe di funzioni: le funzioni unidirezionali con scappatoia.
Queste funzioni y=f(x) sono facili da calcolare mentre la funzione inversa x=f-1(y) non lo è a meno di non conoscere qualche parametro aggiuntivo (scappatoia). Tale parametro aggiuntivo è costituito dalla chiave segreta Ks. La più comune funzione unidirezionale è una biiezione.
4.1 Aritmetica finita per la crittografia
Gli algoritmi necessari per la generazione di chiavi pubbliche si servono di un campo della matematica relativo alla teoria dei numeri. L' aritmetica finita manipola i numeri in modo diverso dall' aritmetica ordinaria, viene chiamata così perchè si usano gli stessi nomi e simboli, ma i valori sono interi e l'insieme dei numeri ha dimensione finita (per gli usi in crittografia tale dimensione sarà molto grande).
L' aritmetica è detta modulo m quando è composta da m differenti valori interi, in particolare se m è un numero primo le proprietà della moltiplicazione sono semplificate perchè in questo caso ogni numero è dotato di inverso unico e distinto.
Si consideri la funzione esponenziale an . La variabile indipendente è n , mentre la base a e il modulo p sono mantenuti costanti.
L' esponente n può essere trattato come numero appartenente all' aritmetica modulo p per cui con degli esempi si comprende che:
an+(p-1)= an modulo p e ciò dimostra la finitezza della dimensione dell' aritmetica.
ap-1= 1 ossia ap = a
Questo è un modo alternativo ad esprimere il teorema di Fermat che ha un ruolo fondamentale sia nella teoria dei numeri che in crittografia.
La funzione esponenziale quindi risulta periodica di periodo p-1, proprio in virtù del fatto che trattiamo n in tale aritmetica. Per semplificare la complessità delle operazioni quindi si possono :
1) ridurre il valore della base a al suo residuo modulo p
2) ridurre l' esponente n al suo residuo modulo p-1.
Per alcuni valori di a, la funzione esponenziale genera una permutazione dell' aritmetica. Per tali valori la funzione quindi è una biiezione. I valori della base con queste proprietà sono detti generatori.
La funzione esponenziale verrà usata quando la base costituisce un generatore dell' aritmetica proprio perchè sarà una biiezione ammettendo l' operazione inversa.
Anche il risultato del logaritmo è un numero intero e rientra nella dimensione p. La funzione esponenziale così come è stata descritta costituisce una funzione unidirezionale.
In crittografia il valore per p è molto grande, in questo modo di rende difficoltosa la costruzione di una tavola logaritmica.Inoltre il calcolo del logaritmo è un' operazione molto complessa. Introdotto questo fondamento teorico, vediamone l' applicazione in un algoritmo asimmetrico.
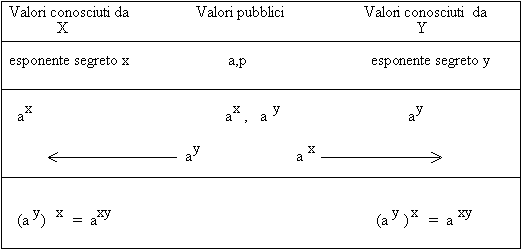
m Due enti comunicanti X,Y scelgono un numero primo p sufficentemente grande, quindi un generatore "a" per l' aritmetica modulo p. Sia a che p sono pubblici.
m Ogni ente genera un numero casuale (che non sia né troppo vicino a 0 né a p) appartenente all' aritmetica. Siano tali valori x per l'ente X e y per Y. Questi valori sono mantenuti segreti.
m Il messaggio viene codificato nella forma esponenziale cioè nel canale transiterà il valore corrispondente ad ax che X invia a Y e il messaggio ay che Y invia ad X.
m L' ultimo passo consiste nel calcolare un ulteriore valore esponenziale: nel caso di X il valore ricevuto ay viene elevato ad x. Entrambe gli enti quindi posseggono il medesimo valore axy.
Tale valore è segreto e può essere utilizzato come chiave comune in un codice simmetrico.
La sicurezza dello schema dipende dalla difficolta di calcolare il logaritmo, infatti un eventuale nemico conosce il generatore a , il modulo p e i valori corrispondenti ad ay o ax e da questi risalire ad x e y attraverso il logaritmo appunto.
Il limite del metodo di distribuzione di chiavi risiede nel fatto che gli enti X e Y non avevano mai comunicato in precedenza e quindi nessuno dei due è sicuro di comunicare realmente con l' altro. Infatti un potenziale nemico che indicheremo con Z potrebbe inserirsi nella comunicazione intercettando i valori ax e ay sostituendo a entrambe il valore az. In questa maniera condividerebbe il numero segreto axz con X e il valore ayz con Y.
Quando l' ente X intende comunicare a Y i messaggi codificati giungono prima all' intruso Z che li decodifica per conoscere il testo chiaro e che ridecodifica per Y. Inoltre utilizzatando troppo a lungo gli stessi valori a e p un nemico potrebbe iniziare a stilare numerose tavole per essere in grado di calcolare il logaritmo di ogni valore ax intercettato.
4.1.2 Codifica senza trasporto di chiavi
Quando è molto difficile calcolare l' inverso della funzione esponenziale y=xz, la funzione potenza corrispondente (cioè y=xz vista come funzione di x) ha la caratteristica di avere come inverso una funzione potenza. Per funzioni potenza modulo p ci sono esponenti che producono reciprocamente la funzione potenza e la sua inversa. Siano m ed n questi esponenti allora succede che:
y = xm implica che x = yn tale che xmn = x modulo p
Poichè i calcoli per l' esponente sono modulo p-1 la condizione per generare funzioni inverse è :
Occorre però un' ulteriore condizione: le funzioni devono avere un solo verso. Per tale motivo si devono scegliere m ed n in modo tale che non abbiano fattori in comune con p-1. Nelle tecniche crittografiche la potenza "n" è tenuta segreta e costituisce la chiave. per risalire ad n occorre calcolare n=logxy e sappiamo essere difficile. Anche m deve essere tenuto segreto perchè attraverso di esso si può trovare n.
Il metodo di codifica utilizzante la funzione potenza permette il transito dei messaggi senza alcun bisogno di trasporto delle chiavi.
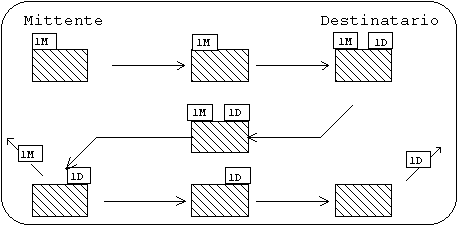
La scatola grande rappresenta il codice che protegge il messaggio, le scatole piccole le chiavi di codifica-decodifica. Il Mittente chiude la scatola con un lucchetto lM tenendo per sè la chiave di apertura. Quando il Destinatario riceve la scatola aggiunge il suo lucchetto lD e rinvia il codice al Mittente. Questo toglie il proprio lucchetto (lM) con la chiave da lui posseduta e rispedisce la scatola con il solo lucchetto lD al Destinatario il quale apre la scatola dopo aver tolto lD. Il tutto quindi è avvenuto senza alcun trasporto di chiavi.
Simbolicamente chiudere la scatola rappresenta codificare il messaggio con la funzione potenza. Per il Mittente il mettere e togliere lM significa applicare la funzione potenza con gli esponenti m ed n soddisfacenti la condizione posta sopra. Una applicazione analoga con valori u,v viene eseguita da parte del Destinatario.
Durante il primo trasporto il messaggio x viene codificato nella forma xm e torna al Mittente doppiamente codificato come xmu .
Questi provvede a rimuovere la sua codifica con l' esponente n, riducendo il messaggio a xu .Quando tale messaggio perviene a Destinatario, può essere decodificato con xuv= x.
Il punto debole di questo metodo risiede però nell' autenticazione, poichè Mittente non è sicuro che il messaggio xm u provenga da Destinatario.
Tale sigla rappresenta le iniziali dei realizzatori (Rivest,Shamir,Adleman) e si avvale di una funzione potenza come descritta sopra:
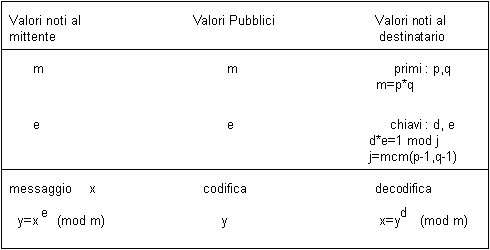
dove "x" rappresenta il testo chiaro, "e" la chiave pubblica, "y" il testo cifrato e "d" la chiave segreta necessaria per la decodifica. In un algoritmo a chiave pubblica però non si può utilizzare un numero p primo per il modulo, poichè le chiavi sono facilmente deducibili la una dall' altra. La novità introdotta dall' RSA consiste nell' usare un numero m non primo. Tale valore deriva dal prodotto di due grandi primi p e q distinti, cioè m=p*q. E' questo il punto forte di tale algoritmo, la grande difficoltà di fattorizzare numeri molto grandi in primi. La chiave pubblica sarà costituita così da m mentre i suoi fattori p e q dovranno rimanere segreti.
La funzione esponente è periodica di periodo j tale che xj+1=x (mod m). E' facile trovare così gli esponenti e ed d per la codifica e la decodifica. La decodifica restituisce il testo originale se:
Il metodo per calcolare il periodo j per qualsiasi valore di m è dato da :
j=mcm(p-1,q-1).
Il minimo comune multiplo si può calcolare dividendo (p-1)(q-1) per il loro MCD. Si ha così un semplice metodo per calcolare le chiavi d ed e partendo solo da p e q.
Potrebbe sorgere qualche dubbio se scegliendo casualmente la chiave di codifica e la funzione y=xe sia biiettiva. La risposta è affermativa se e non ha fattori comuni con p-1 o q-1.
Un medoto di attacco che non si basa sull' individuazione della chiave di decifratura e sulla fattorizzazione di m è il seguente. Con il testo cifrato y si forma il valore ye, il risultato ottenuto viene rielevato ancora ad e. Tale operazione si ripete finchè non si ritrova il testo cifrato y. Si trova in pratica il periodo della funzione e il testo chiaro è dato dall' ultimo valore prima di ritrovare y.
Se l' iterazione completa il ciclo in un numero accettabile di passi, tale attacco può avere successo. Per evitare attacchi iterattivi del genere è necessario imporre la condizione che p (q) siano molto grandi e p-1 non avere solo piccoli fattori altrimenti il calcolo del logaritmo risulta essere possibile.
Sono state svolte accurate analisi sulla corrispondenza tra i valori di p-1 e il numero di passi necessari per decodificare un messaggio, mostrando la sicurezza del metodo RSA.
Uno dei primi metodi per costruire algoritmi a chiave pubblica consisteva nell' usare problemi di conosciuta complessità. Il mittente li formula ed il ricevente li risolve, decodificando così il messaggio. Questo contiene un dato che permette di risolvere velocemente il problema pervenutogli.
L' algoritmo knapsack fa uso di un vettore di n numeri interi E=(E1....En) e di un vettore segreto di cifre binarie M=(M1.....Mn) .
Si calcoli il prodotto scalare M"=E1M1+ ........ +EnMn.
Ora assegnato il valore M" ed il vettore E determinare il vettore M. E rappresenta la chiave pubblica, il messaggio cifrato è M" mentre M è il testo chiaro.
Il problema è specificato dando un vettore di knapsack che è il vettore di interi ed un totale di knapsack che deve essere calcolato. La soluzione consiste nel trovare un sottoinsieme di E che mi dia il valore M".
Algoritmi che sono in grado di dare la soluzione a questo tipo di problemi sono molto complessi.
Il problema si semplifica molto se il vettore E è formato da interi in progressione geometrica, o comunque ogni peso è maggiore della somma dei precedenti (super-increasing sequence).
L' algoritmo crittografico utilizza una caratteristica del genere e affinchè non sia debole occorre che la sequenza di interi e quindi quella binaria abbia grandi dimensioni in modo da rendere inefficente ogni ricerca esaustiva, infatti se la dimensione è n si hanno 2n possibili combinazioni.
Come qualsiasi algoritmo asimmetrico il knapsack comprende un metodo per generare chiavi pubbliche e segrete, un metodo di codifica ed uno di decodifica.
I passi da seguire sono quindi :
ý un eventuale mittente genera le chiavi costruendo un vettore E super-increasing
ý quindi sceglie un modulo m a caso ed un fattore a in maniera tale che MCD(m,a)=1. Attraverso l' algoritmo di Euclide è in grado di trovare l' inverso di a.
ý Quindi costruisce un altro vettore moltiplicando ogni elemento del vettore di partenza per a, il tutto in una aritmetica modulo m.
Il vettore così ottenuto costituisce la chiave pubblica, mentre m, a ed il vettore di partenza E sono la chiave segreta. La codifica consiste nell' usare blocchi di testo come cifre binarie per eseguire il prodotto scalare con il vettore E.
La decodifica consiste nel moltiplicare la somma pervenuta per l' inverso di a, così da ottenere un valore riferito al vettore E di partenza. Ora la soluzione è computazionalmente semplice e rappresenta i pesi che identificano il testo cifrato.