Reaching 3-Connectivity via Edge-edge Additions
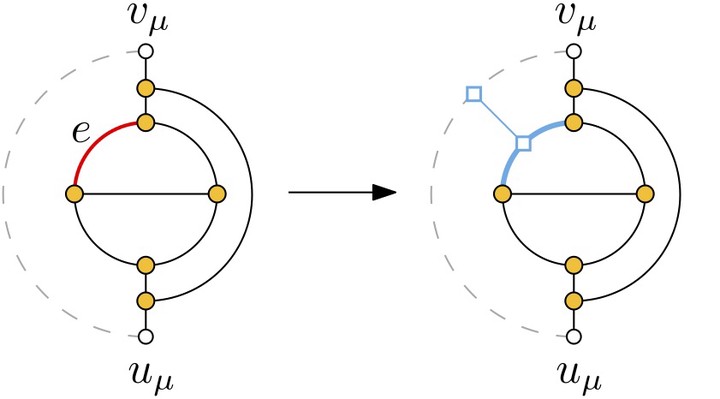 (left) Pertinent graph $pert(\mu)$ of an $e$-externally $3$-connectible S-node $\mu$ and (right) the subdivision of a $3$-connected planar graph obtained by performing an edge-edge addition on $\langle e, (u_\mu,v_\mu)\rangle$ in $pert(\mu)$
(left) Pertinent graph $pert(\mu)$ of an $e$-externally $3$-connectible S-node $\mu$ and (right) the subdivision of a $3$-connected planar graph obtained by performing an edge-edge addition on $\langle e, (u_\mu,v_\mu)\rangle$ in $pert(\mu)$
Abstract
Given a graph $G$ and a pair $\langle e’,e’'\rangle$ of distinct edges of $G$, an edge-edge addition on $\langle e’,e’'\rangle$ is an operation that turns $G$ into a new graph $G'$ by subdividing edges $e'$ and $e'‘$ with a dummy vertex $v'$ and $v'‘$, respectively, and by adding the edge $(v’,v’')$. In this paper, we show that any $2$-connected simple planar graph with minimum degree $\delta(G) \geq 3$ and maximum degree $\Delta(G)$ can be augmented by means of edge-edge additions to a $3$-connected planar graph $G'$ with $\delta(G’) \geq 3$ and $\Delta(G’) = \Delta(G)$, where each edge of $G$ participates in at most one edge-edge addition. This result is based on decomposing the input graph into its $3$-connected components via SPQR-trees and on showing the existence of a planar embedding in which edge pairs from a special set share a common face. Our proof is constructive and yields a linear-time algorithm to compute the augmented graph.
As a relevant application, we show how to exploit this augmentation technique to extend some classical NP-hardness results for bounded-degree $2$-connected planar graphs to bounded-degree $3$-connected planar graphs.