 A planar saturation (left) and the corresponding admissible partition (right)
A planar saturation (left) and the corresponding admissible partition (right)
Abstract
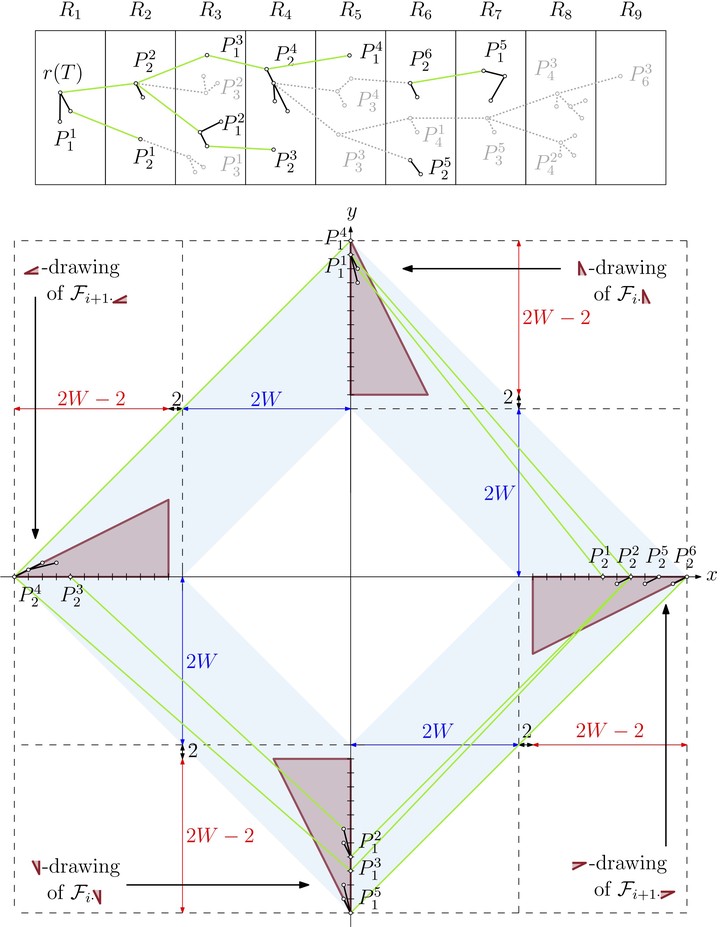
We study the problem of drawing a dynamic graph, where each vertex appears in the graph at a certain time and remains in the graph for a fixed amount of time, called the window size. This defines a graph story, i.e., a sequence of subgraphs, each induced by the vertices that are in the graph at the same time. The drawing of a graph story is a sequence of drawings of such subgraphs. To support readability, we require that each drawing is straight-line and planar and that each vertex maintains its placement in all the drawings. Ideally, the area of the drawing of each subgraph should be a function of the window size, rather than a function of the size of the entire graph, which could be too large.
We show that the graph stories of paths and trees can be drawn on a $2W \times 2W$ and on an $(8W+1) \times (8W+1)$ grid, respectively, where $W$ is the window size. These results are constructive and yield linear-time algorithms. Further, we show that there exist graph stories of planar graphs whose subgraphs cannot be drawn within an area that is only a function of $W$.