Subexponential-Time and FPT Algorithms for Embedded Flat Clustered Planarity
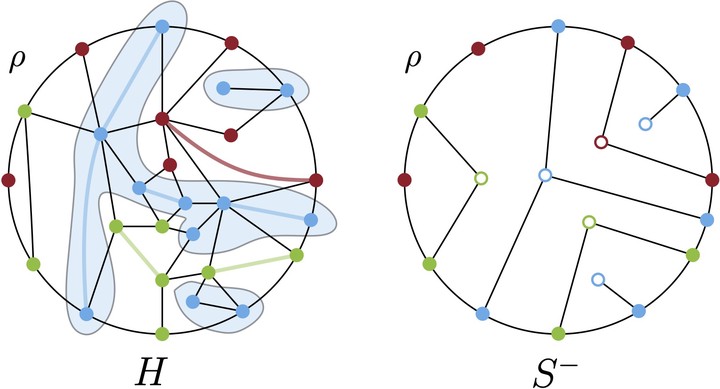 (left) Partial saturation of c-graph $H$ by
(left) Partial saturation of c-graph $H$ by means of candidate saturating edges lying in
the interior of cycle $\rho$.
(right) Cycle-star $S^-$ representing the
cluster-connectivity in the interior of $\rho$
Abstract
The C-Planarity problem asks for a drawing of a clustered graph, i.e., a graph whose vertices belong to properly nested clusters, in which each cluster is represented by a simple closed region with no edge- edge crossings, no region-region crossings, and no unnecessary edge-region crossings. We study C-Planarity for embedded flat clustered graphs, graphs with a fixed combinatorial embedding whose clusters partition the vertex set. Our main result is a subexponential-time algorithm to test C-Planarity for these graphs when their face size is bounded. Furthermore, we consider a variation of the notion of embedded tree decomposition in which, for each face, including the outer face, there is a bag that contains every vertex of the face. We show that C-Planarity is fixed-parameter tractable with the embedded-width of the the underlying graph and the number of disconnected clusters as parameters.