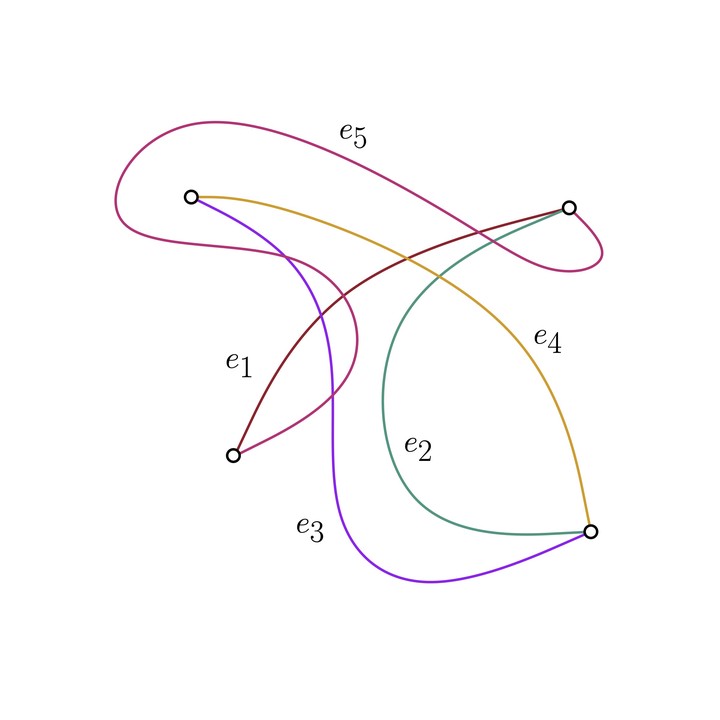
 An $omega$-streamed graph that is $\omega$-stream planar for $\omega=2$
An $omega$-streamed graph that is $\omega$-stream planar for $\omega=2$
Abstract
In this research we introduce a notion of planarity for graphs that are presented in a streaming fashion. A streamed graph is a stream of edges $e_1,e_2,\dots,e_m$ on a vertex set $V$. A streamed graph is $\omega$-stream planar with respect to a positive integer window size $\omega$ if there exists a sequence of planar topological drawings $\Gamma_i$ of the graphs $G_i=(V,{e_j \mid i\leq j < i+\omega})$ such that the common graph $G^{i}\cap=G_i\cap G{i+1}$ is drawn the same in $\Gamma_i$ and in $\Gamma_{i+1}$, for $1\leq i < m-\omega$. The Stream Planarity Problem with window size $\omega$ asks whether a given streamed graph is $\omega$-stream planar. We also consider a generalization, where there is an additional backbone graph whose edges have to be present during each time step. These problems are related to several well-studied planarity problems.
We show that the Stream Planarity Problem is $\mathcal{NP}$-complete even when the window size is a constant and that the variant with a backbone graph is $\mathcal{NP}$-complete for all $\omega \ge 2$. On the positive side, we provide $O(n+\omega{}m)$-time algorithms for (i) the case $\omega = 1$ and (ii) all values of $\omega$ provided the backbone graph consists of one $2$-connected component plus isolated vertices and no stream edge connects two isolated vertices. Our results improve on the Hanani-Tutte-style $O((nm)^3)$-time algorithm proposed by Schaefer [GD’14] for $\omega=1$.