3-coloring arrangements of line segments with 4 slopes is hard
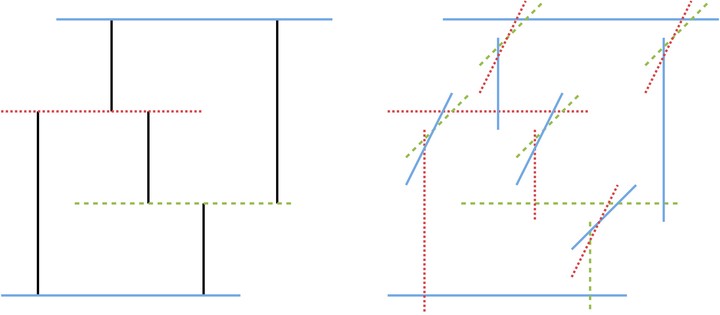(left) A visibility representation $\Gamma$ of a planar graph $G$ whose horizontal segments are colored according to a $3$-coloring of $G$, and (right) a $3$-coloring of an arrangement of line segments with $4$ slopes computed from $\Gamma$
Abstract
In a paper first appeared at SODA ’04, Eppstein proved that testing the $3$-colorability of arrangements of line segments is an NP-complete problem. However, if the slopes of the segments are limited to three different values, a $3$-coloring can be trivially obtained by assigning the same color to all the segments having the same slope.
We thus study the complexity of testing the $3$-colorability of arrangements of line segments, or equivalently of their intersection graphs, that are restricted to have a constant number $s > 3$ of slopes, and prove that this remains NP-complete even for $s = 4$, which is hence tight. More in general, we prove that $k$-coloring arrangements of line segments is NP-complete even if the segments have at most $k + 1$ slopes.
Since the problem of computing a $k$-coloring of an arrangement of line segments is equivalent to computing the constrained geometric thickness of a straight-line drawing of a graph in the plane, our result extends to this problem.