How to Morph Planar Graph Drawings
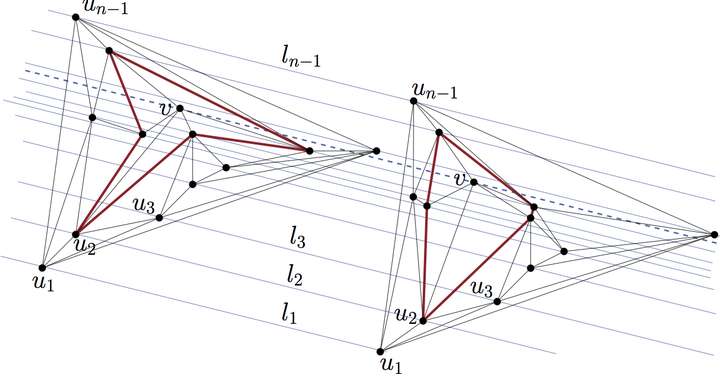 Illustration of the “Fast Convexifier” procedure
Illustration of the “Fast Convexifier” procedure
Abstract
Given an $n$-vertex graph and two straight-line planar drawings of the graph that have the same faces and the same outer face, we show that there is a morph (i.e., a continuous transformation) between the two drawings that preserves straight-line planarity and consists of $O(n)$ steps, which we prove is optimal in the worst case. Each step is a unidirectional linear morph, which means that every vertex moves at constant speed along a straight line, and the lines are parallel although the vertex speeds may differ. Thus we provide an efficient version of Cairns’ 1944 proof of the existence of straight-line planarity-preserving morphs for triangulated graphs, which required an exponential number of steps.
Type
Publication
SIAM Journal on Computing