Approximation Algorithms for Facial Cycles in Planar Embeddings
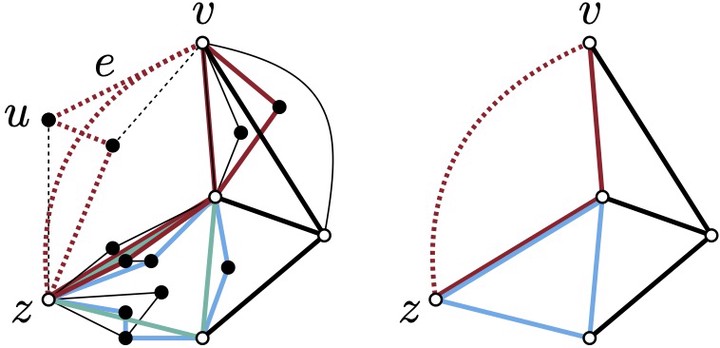 (left) A planar graph $G$ with a red and a blue cycle. (right) The skeleton of an R-node $\mu$ of the SPQR-tree of $G$ rooted at edge $e=uv$. The blue and red cycles are relevant for $\mu$ as they project to the blue and red cycle of the skeleton, respectively. The red cycle is an interface cycle
(left) A planar graph $G$ with a red and a blue cycle. (right) The skeleton of an R-node $\mu$ of the SPQR-tree of $G$ rooted at edge $e=uv$. The blue and red cycles are relevant for $\mu$ as they project to the blue and red cycle of the skeleton, respectively. The red cycle is an interface cycle
Abstract
Consider the following combinatorial problem$:$ Given a planar graph $G$ and a set of simple cycles $\mathcal C$ in $G$, find a planar embedding $\mathcal E$ of $G$ such that the number of cycles in $\mathcal C$ that bound a face in $\mathcal E$ is maximized. This problem, called Max Facial $\mathcal C$-Cycles, was first studied by Mutzel and Weiskircher [IPCO ‘99] and then proved NP-hard by Woeginger [Oper. Res. Lett., 2002].
We establish a tight border of tractability for Max Facial $\mathcal C$-Cycles in biconnected planar graphs by giving conditions under which the problem is NP-hard and showing that strengthening any of these conditions makes the problem polynomial-time solvable. Our main results are approximation algorithms for Max Facial $\mathcal C$-Cycles. Namely, we give a $2$-approximation for series-parallel graphs and a $(4+\varepsilon)$-approximation for biconnected planar graphs. Remarkably, this provides one of the first approximation algorithms for constrained embedding problems.