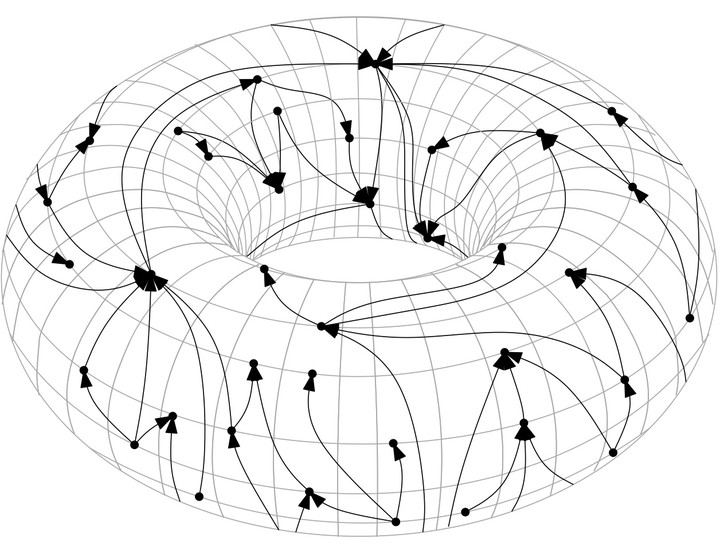
A level embedding on the surface of the torus
Abstract
In this paper we settle the computational complexity of two open problems related to the extension of the notion of level planarity to surfaces different from the plane. Namely, we show that the problems of testing the existence of a level embedding of a level graph on the surface of the rolling cylinder or on the surface of the torus, respectively known by the name of Cyclic Level Planarity and Torus Level Planarity, are polynomial-time solvable.
Moreover, we show a complexity dichotomy for testing the Simultaneous Level Planarity of a set of level graphs, with respect to both the number of level graphs and the number of levels.
Giordano Da Lozzo
Assistant Professor (RTDb)
My research interests are in Algorithm Engineering and Complexity, focused in particular on the theoretical and algorithmic challenges arising from the visualization of graphs.