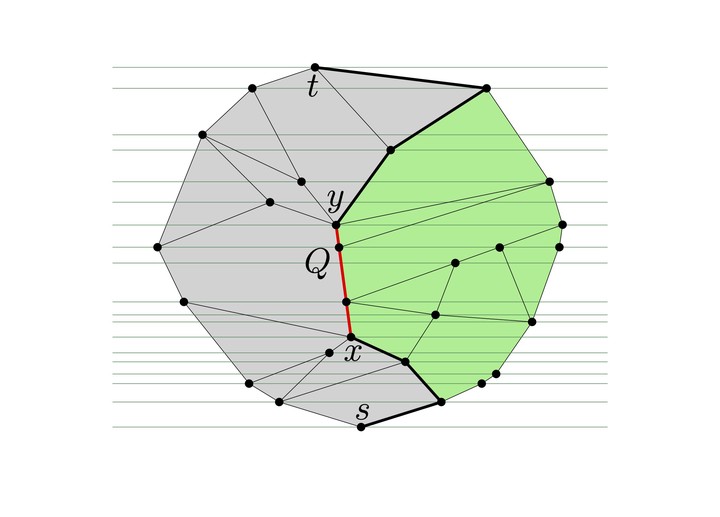
 A left-flat path $Q$ (red thick line) and its elongation $E(Q)$ (red and black thick lines)
A left-flat path $Q$ (red thick line) and its elongation $E(Q)$ (red and black thick lines)
Abstract
We give an algorithm to compute a morph between any two convex drawings of the same plane graph. The morph preserves the convexity of the drawing at any time instant and moves each vertex along a piecewise linear curve with linear complexity. The linear bound is asymptotically optimal in the worst case.
Type
Publication
In 31st International Symposium on Computational Geometry (SoCG 2015)