The Importance of Being Proper - (In Clustered-Level Planarity and T-Level Planarity)

Patrizio Angelini, Giordano Da Lozzo, Giuseppe Di Battista, Maurizio Patrignani, Fabrizio Frati, Vincenzo Roselli

2014-06-01

Project Slides DOI GD 2014 Theor. Comp. Science ArXiv

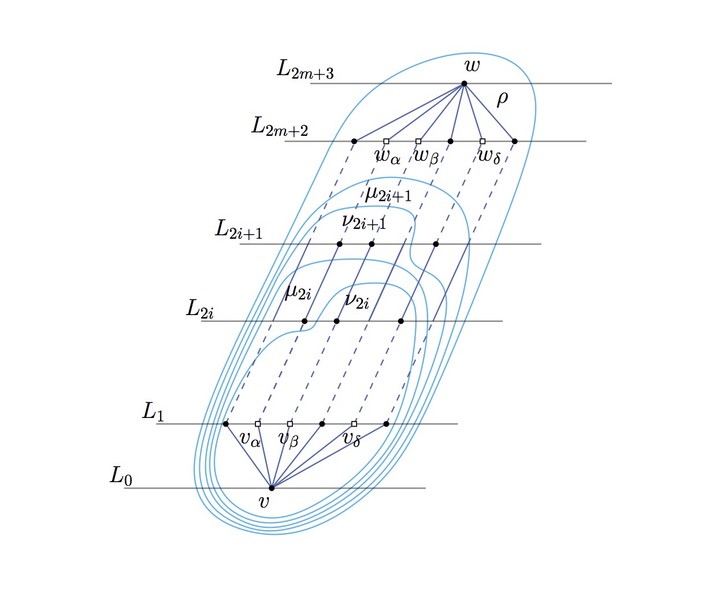Clustered-Level Planarity is $\mathcal{NP}$-complete. Reduction focused on the i-th triple $\langle \alpha,\beta,\delta\rangle$

Abstract

In this paper we study two problems related to the drawing of level graphs, that is, $T$-Level Planarity and Clustered-Level Planarity. We show that both problems are $\mathcal{NP}$-complete in the general case and that they become polynomial-time solvable when restricted to proper instances.

Type

Conference paper

Publication

In 22nd International Symposium on Graph Drawing and Network Visualization (GD 2014)

Level Planarity Clustered Planarity