Definition
An instance x of the data type real is an algebraic real number.
There are many ways to construct a real:
either by conversion from double, bigfloat, integer or rational
or by applying one of the arithmetic operators
+ , - ,*,/ or
![]() to
real numbers.
One may test the sign of a real number or compare two real numbers by
any of the comparison relations
= ,! = , < , < = , > and > =.
The outcome of such a test is exact.
There is also a non-standard version of the sign function: the call
x.sign(integer q)
computes the sign of x under the precondition
that
| x| < = 2-q implies x = 0.
This version of the sign function allows the user to assist the data type in the
computation of the sign of x, see the example below.
to
real numbers.
One may test the sign of a real number or compare two real numbers by
any of the comparison relations
= ,! = , < , < = , > and > =.
The outcome of such a test is exact.
There is also a non-standard version of the sign function: the call
x.sign(integer q)
computes the sign of x under the precondition
that
| x| < = 2-q implies x = 0.
This version of the sign function allows the user to assist the data type in the
computation of the sign of x, see the example below.
There are several functions to compute approximations of reals.
The calls to_bigfloat(x) and x.get_bigfloat_error() return bigfloats
xnum and xerr such that
| xnum - x| < = xerr.
The user may set a bound on xerr.
More precisely, after the call x.improve_approximation_to(integer q) the
data type guarantees
xerr < = 2-q.
One can also ask for double approximations of a real number x.
The calls to_double(x) and x.get_double_error() return doubles xnum and
xerr such that
| xnum - x| < = | xnum|*xerr.
Note that
xerr = ![]() is possible.
is possible.
#include < LEDA/real.h >
Creation
reals may be constructed from data types double, bigfloat, long, int and integer. The default constructor real() initializes the real to zero.
Operations
| double | to_double(real) | returns the current double approximation of x. |
| bigfloat | to_bigfloat(real) | returns the current bigfloat approximation of x. |
| double | x.get_double_error() | returns the relative error of the current double approximation of x, i.e., | x - todouble(x)| is bounded by x.get_double_error()*| to_double(x)|. |
| bigfloat | x.get_bigfloat_error() | returns the absolute error of the current bigfloat approximation of x, i.e., | x-to_bigfloat(x)| is bounded by x.get_bigfloat_error(). |
| int | sign(real x) | returns the sign of (the exact value of) x. |
| int | x.sign(integer q) | as above. Precondition: if | x| < = 2-q then x = 0. |
| void | x.improve_approximation_to(integer q) | |
| (re-)computes the approximation of x such that x.get_bigfloat_error() < = 2-q after the call x.improve_approximation_to(q). | ||
| void | x.compute_with_precision(long k) | |
| (re-)computes the approximation of x; each numerical operation is carried out with k binary places. | ||
| void | x.guarantee_relative_error(long k) | |
| (re-)computes an approximation of x such that the relative error of the approximation is less than 2-k. | ||
| ostream& | ostream& O << x | writes the closest interval that is known to contain x to the output stream O |
| istream& | istream& I >> real& x | reads real number x from the output stream I (in double format) |
| real | sqrt(real x) | |
| real | root(real x, int d) |
Precondition: d > = 2 |
| real | abs(real x) | absolute value of x |
| real | sqr(real x) | square of x |
| real | dist(real x, real y) | euclidean distance of vector (x,y) to the origin |
| real | powi(real x, int n) | n.th power of x |
Implementation
A real is represented by the expression which defines it and a double
approximation x' together with a relative error bound
![]() .
The arithmetic operators +, -, *, /,
.
The arithmetic operators +, -, *, /,
![]() take constant time.
When the sign of a real number needs to be determined, the data type first
computes a number q, if not already given as an argument to sign, such that
| x| < = 2-q implies x = 0.
The bound q is computed as described in [55].
take constant time.
When the sign of a real number needs to be determined, the data type first
computes a number q, if not already given as an argument to sign, such that
| x| < = 2-q implies x = 0.
The bound q is computed as described in [55].
Using bigfloat artihmetic, the data type then computes an interval I of maximal length 2-q that contains x. If I contains zero, then x itself is equal to zero. Otherwise, the sign of any point in I is returned as the sign of x.
Two shortcuts are used to speed up the computation of the sign. Firstly, if the double approximation already suffices to determine the sign, then no bigfloat approximation is computed at all. Secondly, the bigfloat approximation is first computed only with small precision. The precision is then doubled until either the sign can be decided (i.e., if the current approximation interval does not contain zero) or the full precision 2-q is reached.
Example
We give two examples of the use of the data type real. The examples deal with the Voronoi diagram of line segments and the intersection of line segments, respectively.
The following incircle test arises in the computation of Voronoi diagrams of line segments [15,13]. For i, 1 < = i < = 3, let li : aix + biy + ci = 0 be a line in two-dimensional space and let p = (0, 0) be the origin. In general, there are two circles passing through p and touching l1 and l2. The centers of these circles have homogeneuos coordinates (xv, yv, zv), where
| xv | = | a1c2 + a2c1 |
|
| yv | = | b1c2 + b2c1 |
|
| zv | = |
and
| s | = | b1D2 - b2D1, | N | = | (a12 + b12)(a22 + b22) |
| r | = | a1D2 - a2D1, | D | = | a1a2 - b1b2. |
Let us concentrate on one of these (say, we take the plus sign in both cases). The test whether l3 intersects, touches or misses the circle amounts to determining the sign of
E : = dist2(v, l3) - dist2(v, p) = 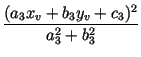 - (xv2 + yv2).
- (xv2 + yv2). |
The following program computes the sign of
![]() : = (a32 + b32)*E using our data type real.
: = (a32 + b32)*E using our data type real.
int INCIRCLE( real a1, real b1, real c1, real a2, real b2, real c2, real a3, real b3, real c3 )
{
real;
real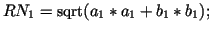
real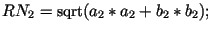
real A = a1*c2 + a2*c1;
real B = b1*c2 + b2*c1;
real C = 2*c1*c2;
real D = a1*a2 - b1*b2;
real s = b1*RN2 - b2*RN1;
real r = a1*RN2 - a2*RN1;
int signx = sign(s);
int signy = sign(r);
real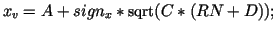
real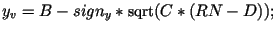
real zv = RN - (a1*a2 + b1*b2);
real P = a3*xv + b3*yv + c3*zv;
real D32 = a3*a3 + b3*b3;
real R2 = xv*xv + yv*yv;
real E = P*P - D32*R2;
return sign(E);
}
We can make the above program more efficient if all coefficients ai, bi and ci,
1 < = i < = 3, are k bit integers, i.e.,
integers whose absolute value is bounded by 2k - 1. In
[15,13] we showed that for
![]() ! = 0
we have
|
! = 0
we have
|![]() | > = 2-24k - 26. Hence we may add a
parameter int k in the above program and replace the last line by
| > = 2-24k - 26. Hence we may add a
parameter int k in the above program and replace the last line by
![]()
Without this assistance,
reals automatically compute a weaker bound of
|![]() | > = 2-56k - 161 for
| > = 2-56k - 161 for
![]() ! = 0 by [14].
! = 0 by [14].
We turn to the line segment intersection problem next. Assume that all endpoints have k-bit integer homogeneous coordinates. This implies that the intersection points have homogeneous coordinates (X, Y, W) where X, Y and W are (4 k + 3) - bit integers. The Bentley-Ottmann plane sweep algorithm for segment intersection [59] needs to sort points by their x-coordinates, i.e., to compare fractions X1/W1 and X2/W2 where X1, X2, W1, W2 are as above. This is tantamount to determining the sign of the 8k + 7 bit integer X1*W2 - X2*W1. If all variables Xi, Wi are declared real then their sign test will be performed quite efficiently. First, a double approximation is computed and then, if necessary, bigfloat approximations of increasing precision. In many cases, the double approximation already determines the sign. In this way, the user of the data type real gets the efficiency of a floating point filter [31,60] without any work on his side. This is in marked contrast to [31,60] and will be incorporated into [59].