|
Introduction
GAPI provides the application developer with an impressive array of facilities for managing and drawing graphs. The full set of methods of GAPI is given in the reference guide. The purpose of this tutorial is to quickly allow the user to handle the basic features of GAPI.
The available methods have clear names and are easy to use. For example, if you have to construct a new graph, simply use the primitives that the class undi_graph puts at disposal of the programmer to insert nodes and edges (new_node and new_edge). If some edges are directed give to them the desired direction (make_directed). Namely, suppose that you want to create a graph with four nodes (labeled 1,2,3,and 4) and four edges ((1,2),(1,3),(1,4),(2,3)).
- Perform the following sequence of steps:
undi_graph ug;
// create an empty graph called ug
node v1 = ug.new_node(1);
// add a node with identifier 1 to ug
node v2 = ug.new_node(2);
node v3 = ug.new_node(3);
node v4 = ug.new_node(4);
edge e1 = ug.new_edge(v1,v2);
// add an edge to ug
edge e2 = ug.new_edge(v1,v3);
edge e3 = ug.new_edge(v1,v4);
edge e4 = ug.new_edge(v2,v3);
- If some edges are directed, then it can be simply stated as follows.
ug.make_directed(e2,v1);
// edge e2 is directed from v1 to v3
Erasing a node or an edge is also very simple. For example, if you want to delete vertex v2, you can do:
-
ug.del_node(v2);
// edges incident to v2 are automatically deleted
Identifiers associated to nodes and edges can be changed. Of course, collisions with existing identifiers must be avoided.
-
ug.assign_id(v1,84);
// the identifier associated to v1 is changed to 84
When you create a node or an edge, if you do not specify an identifier, then the system automatically selects a non-already-used identifier and associetes it to the new object.
The full set of methods of the classes of GAPI are given in the reference guide. They are grouped into types. We distinguish among constructors and operators, access methods, update methods, and input/output methods
Orthogonal Drawings
Orthogonal drawings have an impressive range of applicability. In what follows we show how to use GAPI for constructing orthogonal drawings.
First, we present a simple strategy, suitable for beginners (but still powerful enough to cover several applications). Second, we show how to work
if performance is more important than aesthetics.
Third, we describe how to behave if aesthetics are more
important than performance.
Fourth, we show how several choices are available for constructing drawings that are more or less compact. Finally, we show how to customize the drawing according to your special requirements.
A simple strategy
If you want to construct an orthogonal drawing of a graph with GAPI, simply do the following:
- Construct your graph by using the primitives that the class undi_graph puts at disposal of the programmer to insert nodes and edges (new_node and new_edge). If some edges are directed give to them the desired direction (make_directed). Suppose that the variable corresponding to the graph is named "ug".
- Perform the following sequence of steps:
plan_undi_graph pug(ug);
orth_plan_undi_graph opug(pug);
draw_undi_graph dug(opug);
The meaning of such steps is the following:
Constructor plan_undi_graph performs a "planarization" of the graph: an order is choosen for the edges around each node trying to keep the number of crossings between edges as low as possible. The name of the planarized graph so obtained is "pug". Variable "pug" is an object of the class plan_undi_graph.
Constructor orth_plan_undi_graph performs an "orthogonalization" of the planarized graph. Each edge is assigned with a specific shape, with the minimum number of bends along the edges. The name of the orthogonal graph so obtained is "opug". Variable "opug" is an object of the class orth_plan_undi_graph.
Constructor draw_undi_graph constructs the final drawing by assigning each node with a position of the plane and each edge-segment with a length. The constructor has the target of using as less area as possible. Variable "dug" is an object of the class draw_undi_graph.
- At this point variable "dug" stores all the information that is needed to draw "ug" as an orthogonal drawing. For example, applying center to node "v" returns the coordinates of the center of "v".
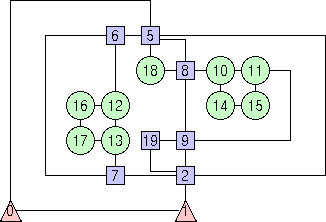
An example of orthogonal drawing constructed with the previous steps is shown in the following figure.
If performance is more important than aesthetics
If you have strict performance requirements, then you can customize the simple piece of code shown above to obtain drawings that are slightly worse either in terms of number of bends along edges or in terms of global area occupied by the drawing. On the other hand you will have better time performance. GDT offers several facilities to explore the performance/effectiveness trade-off.
For example, if you accept to have more bends that those that are strictly needed, you can replace
orth_plan_undi_graph opug(pug);
with
orth_plan_undi_graph opug(pug, PLAN_ORTH_QUICK);
This replaces the default algorithm for orthogonalization with a faster one.
Note: the current version of GDT allows to apply option PLAN_ORTH_QUICK only to graphs that are biconnected and whose nodes have at most four incident edges. A graph is biconnected if the removal of one node is not sufficient to cut it into two (or more) disconnected pieces.
As another example, if you accept to have a larger area than the one that is strictly needed, you can replace
draw_undi_graph dug(opug);
with
draw_undi_graph dug(opug, FAST_COMPACTION);
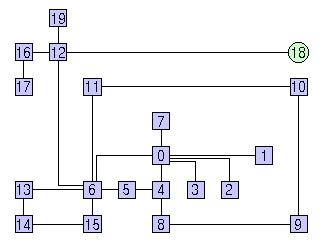
This replaces the default algorithm used in the last step with a faster one. An example of orthogonal drawing constructed with the FAST_COMPACTION option is shown in the following figure.
The same graph drawn with the default algorithm is as follows
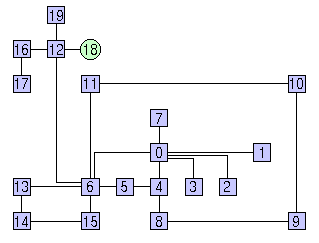
GDT offers other alternatives to FAST_COMPACTION allowing to choose different trade-offs between performance and aesthetics. Namely, FAST_COMPACTION_REFINED, SLOW_COMPACTION, and SLOW_COMPACTION_REFINED (default option).
If aesthetics are more important than performance
If you have strict aesthetics requirements, then you can customize the simple piece of code shown above to obtain drawings that are much better in terms of number of bends along edges. On the other hand you will have worse time performance. For example, you can replace
orth_plan_undi_graph opug(pug);
with
orth_plan_undi_graph opug(pug, PLAN_ORTH_SLOW);
This replaces the default algorithm for orthogonalization with a more accurate one.
An orthogonal drawing constructed with option PLAN_ORTH_SLOW of the same graph of a previous figure is shown below.

Note: the current version of GDT allows to apply option PLAN_ORTH_SLOW only to graphs that are biconnected. A graph is biconnected if the removal of one node is not sufficient to cut it into two (or more) disconnected pieces.
Note: option PLAN_ORTH_SLOW causes the invocation of a branch and bound algorithm, that is potentially exponential in time requirement. This makes it unsuitable for graphs with more that 100 nodes.
Drawing compaction
Several strategies are available for compacting orthogonal drawings. They have assigned constants:
FAST_COMPACTION,
FAST_COMPACTION_REFINED,
SLOW_COMPACTION,
SLOW_COMPACTION_REFINED,
FAST_REGULAR_COMPACTION_1,
SLOW_REGULAR_COMPACTION_1,
FAST_REGULAR_COMPACTION_2,
SLOW_REGULAR_COMPACTION_2,
FAST_REGULAR_COMPACTION_1_REFINED,
SLOW_REGULAR_COMPACTION_1_REFINED,
FAST_REGULAR_COMPACTION_2_REFINED, and
SLOW_REGULAR_COMPACTION_2_REFINED.
If no specification is given, then compaction SLOW_REGULAR_COMPACTION_2_REFINED is applied as a default. If you want to force GDtoolkit to use a certain compaction strategy, different from the default one, you have to specify it as follows:
plan_undi_graph pug(ug);
orth_plan_undi_graph opug(pug);
draw_undi_graph dug(opug,SLOW_COMPACTION);
In this case GAPI will use the compaction strategy SLOW_COMPACTION. Usually, the best strategies, from the aesthetics point of view, are SLOW_REGULAR_COMPACTION_1_REFINED and SLOW_REGULAR_COMPACTION_2_REFINED. On the other hand they are more time consuming than the others. They are strongly recommended for applications where having very compact drawings is a strict requirement.
Drawing customization
If you need to customize your drawing, then you can exploit the capability of GDT in handling user-specified constraints.
For example, if you want that all the nodes of a certain set (that, for example, are the "boundary" of your application) are drawn on the border of the polygon surrounding the drawing (external face) then you can do the following steps:
- Suppose that "ug" is your graph and that "Le" is the list of the nodes of the above set. First, you have to perform:
ug.new_constraint_same_face_node(Le,c)
Where "c" is an integer label that you use to denote the face where the nodes in "Le" will be placed.
- Perform the following sequence of steps:
plan_undi_graph pug(ug);
Determine a face "f" of "pug" containing all the nodes in "Le"; orth_plan_undi_graph opug(pug,f);
draw_undi_graph dug(opug);
During the execution of plan_undi_graph, the constraint is taken into account. Once "pug" is computed, "f" can be determined by simply scanning the faces containing the nodes of "Le". For example you can exploit method node_belongs_to_face that is offered by class plan_undi_graph.
- At this point variable "dug" stores all the information that is needed to draw "ug" as an orthogonal drawing with the nodes in "Le" on the external face.
An orthogonal drawing of the previous graph, constructed with a specific set of nodes (0, 5, and 6) on the external face is shown in the following figure.
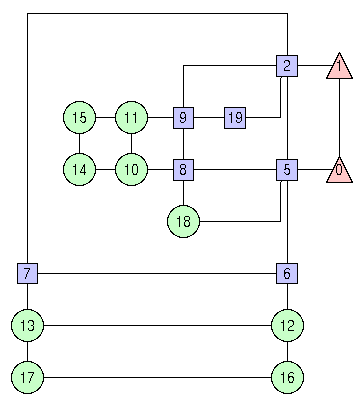
As another example, if you want to emphasize an edge "e" that for some reason is expecially important, then you maight want to preserve it to have crossings and maybe to have bends. This is done very easily by performing ug.new_constraint_uncrossable_edge(e) and/or ug.new_constraint_number_of_bends_on_edge(e,NONE) before performing the planarization step.
You can also specify the width and the height of each node, by simply using the following commands ug.new_constraint_node_width(v,width) and/or ug.new_constraint_node_height(v,height) before performing any orthogonal layout algorithm. What follows is an example of orthogonal drawing in which we have set the width and the height of node 8 both equal to 1, and the width and the height of node 2 equal to 1 and equal to 3, respectively. The length are in terms of integer grid points, and the width and the height of any node are always equal to 0 if not specified otherwise.
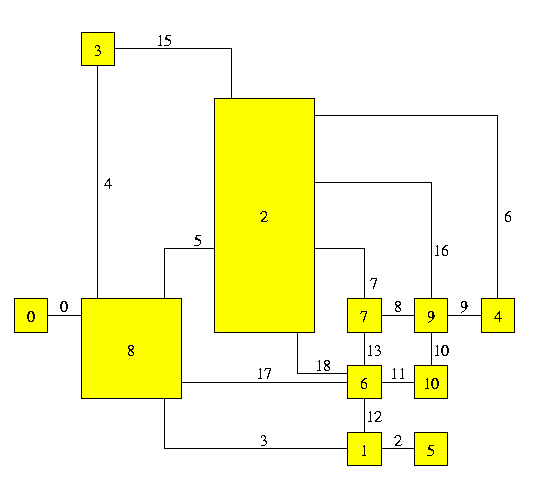
Polyline drawings
GAPI provides algorithms to draw graphs with polygonal edges. If you want to construct a polyline drawing of a graph with GAPI, simply do the following:
- Construct your graph by using the primitives that the class undi_graph puts at disposal of the programmer to insert nodes and edges (new_node and new_edge). If some edges are directed give to them the desired direction (make_directed). Suppose that the variable corresponding to the graph is named "ug".
- Perform the following sequence of steps:
plan_undi_graph pug(ug);
draw_undi_graph dug(pug,POLYLINE);
The meaning of such steps is the following:
Constructor plan_undi_graph performs a "planarization" of the graph: an order is choosen for the edges around each node trying to keep the number of crossings between edges as low as possible. The name of the planarized graph so obtained is "pug". Variable "pug" is an object of the class plan_undi_graph.
Constructor draw_undi_graph constructs the final drawing by assigning each node with a position of the plane and each edge-segment with a length. Variable "dug" is an object of the class draw_undi_graph.
- At this point variable "dug" stores all the information that is needed to draw "ug" as an orthogonal drawing. For example, applying center to node "v" returns the coordinates of the center of "v".
Observe that if you have strict aesthetics requirements, you can replace
draw_undi_graph dug(pug, POLYLINE);
with
draw_undi_graph dug(pug, POLYLINE_COMPACTED);
in order to reduce the total edge-length of the drawing.
Note: the current version of GDT allows to apply option POLYLINE only to graphs that are biconnected. A graph is biconnected if the removal of one node is not sufficient to cut it into two (or more) disconnected pieces.
Examples of polyline representations drawn with GAPI are shown in the following figure:
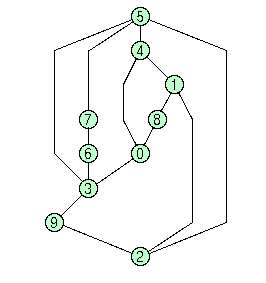
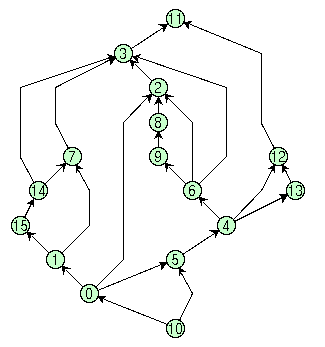
Upward drawings
Upward drawings can be used in several applications, for example to draw Petri Nets or SADT diagrams. GAPI considers a more general model of upward drawing, in which some feedback edges are allowed when an upward drawing does not exist for the given graph. We call such a model "quasi-upward" drawing. In a quasi-upward drawing we call "bend" a point in which a feedback edge is tangent to the horizontal line through this point. In what follows we show how to use GAPI for constructing quasi-upward drawings.
First, we present a simple strategy, suitable for beginners (but still powerful enough to cover several applications).
Second, we show how to work if performance is more
important than aesthetics.
Third, we describe how to behave if aesthetics are more
important than performance.
Finally, we show how to customize the drawing according to your special requirements
A simple strategy
If you want to construct a quasi-upward drawing of a graph with GAPI, simply do the following:
- Construct your graph by using the primitives that the class undi_graph puts at disposal of the programmer to insert nodes and edges (new_node and new_edge). Give each edge the desired direction (make_directed). Suppose that the variable corresponding to the graph is named "ug".
- Perform the following sequence of steps:
list<edge> Le = ug.make_embedding_cand_expanded();
forall (e,Le) ug.new_constraint_uncrossable_edge (e);
plan_undi_graph pug(ug);
pug.contract();
upwa_plan_undi_graph upug(pug);
draw_undi_graph dug(opug);
The meaning of such steps is the following:
Operation ug.make_embedding_cand_expanded() finds an ordering of the edges
around each node such that all edges leaving the node are consecutive, as well as all edges
entering the node. Then it replaces each node "v" with two nodes
"v1" and "v2" such that "v1" has only the edges
entering "v" and "v2" has only the edges leaving "v";
finally, a directed dummy edge from "v1" to "v2" is added, and it is stored
in the list "Le".
Cycle forall (e,Le) ug.new_constraint_uncrossable_edge (e) adds a set of
constraints in order to avoid crossings on the edges of the list "Le" during
the next step.
Constructor plan_undi_graph performs a "planarization" of the
graph: an order is choosen for the edges around each node trying to keep the number of
crossings between edges as low as possible.
The name of the planarized graph so obtained is "pug".
Variable "pug" is an object of the class plan_undi_graph.
Operation pug.contract() restores the original graph by contracting previously
split nodes, preserving the ordering of the edges around nodes.
Constructor upwa_plan_undi_graph computes a quasi-upward representation of
the planarized graph, minimizing the total number of bends along edges.
The name of the quasi-upward graph so obtained is "upug".
Variable "upug" is an object of the class upwa_plan_undi_graph.
Constructor draw_undi_graph constructs the final drawing by assigning each node
with a position of the plane and each edge-segment with a length.
The constructor has the target of using as less area as possible.
Variable "dug" is an object of the class draw_undi_graph.
- At this point variable "dug" stores all the information that is needed to draw "ug" as a quasi-upward drawing. For example, applying center to node "v" returns the coordinates of the center of "v".
An example of quasi-upward drawing constructed with the previous steps is shown in the following figure. Smoothed edges can be used, instead of polygonal edges, computing them as bezier-curves interpolating polylines. GAPI offers the dug.draw(W,true) method to draw "dug" with smoothed edges in a LEDA-window "W"

If performance is more important than aesthetics
If you have strict performance requirements, then you can customize the simple piece of code shown above to obtain drawings that are slightly worse in terms of global edge length used by the drawing. On the other hand you will have better time performance. To do it, you can replace
draw_undi_graph dug(upug);
with
draw_undi_graph dug(upug, FAST_COMPACTION);
An example of quasi-upward drawing constructed with the FAST_COMPACTION option ia shown in the followin figure:
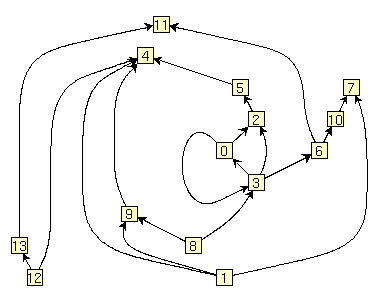
The same graph drawn with the default algorithm is as follows:

If aesthetics are more important than performance
If you have strict aesthetics requirements, then you can customize the simple piece of code shown above to obtain drawings that are much better in terms of number of bends along edges. On the other hand you will have worse time performance. For example, you can replace
upwa_plan_undi_graph upug(pug);
with
upwa_plan_undi_graph upug(pug, PLAN_UPWARD_SLOW);
This replaces the default algorithm for quasi-upward with a more accurate one.
A quasi-upward drawing constructed with option PLAN_UPWARD_SLOW of the same graph of a previous figure is shown below.
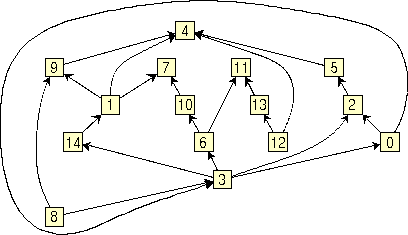
Note: the current version of GDT allows to apply option PLAN_UPWARD_SLOW only to graphs that are biconnected. A graph is biconnected if the removal of one node is not sufficient to cut it into two (or more) disconnected pieces.
Note: option PLAN_UPWARD_SLOW causes the invocation of a branch and bound algorithm, that is potentially exponential in time requirement. This makes it unsuitable for graphs with more that 100 nodes.
Drawing customization
If you need to customize your drawing, then you can exploit the capability of GDT in handling user-specified constraints.
For example, if you want that all the nodes of a certain set (that, for example, are the "boundary" of your application) are drawn on the border of the polygon surrounding the drawing (external face) then you can do the following steps:
- Suppose that "ug" is your graph and that "Le" is the list of the nodes of the above set. First, you have to perform:
ug.new_constraint_same_face_node(Le,c)
Where "c" is an integer label that you use to denote the face where the nodes in "Le" will be placed.
- Perform the following sequence of steps:
plan_undi_graph pug(ug);
Determine a face "f" of "pug" containing all the nodes in "Le"; upwa_plan_undi_graph upug(pug,f);
draw_undi_graph dug(upug);
During the execution of plan_undi_graph, the constraint is taken into account. Once "pug" is computed, "f" can be determined by simply scanning the faces containing the nodes of "Le". For example you can exploit method node_belongs_to_face that is offered by class plan_undi_graph.
- At this point variable "dug" stores all the information that is needed to draw "ug" as a quasi-upward drawing with the nodes in "Le" on the external face.
As another example, if you want to emphasize an edge "e" that for some reason is expecially important, then you maight want to preserve it to have crossings and maybe to have bends. This is done very easily by performing ug.new_constraint_uncrossable_edge(e) and/or ug.new_constraint_number_of_bends_on_edge(e,NONE) before performing the planarization step.
Visibility drawings
GAPI provides several visibility layout algorithms. If you want to construct a standard visibility representation of a graph with GAPI, simply do the following:
- Construct your graph by using the primitives that the class undi_graph puts at disposal of the programmer to insert nodes and edges (new_node and new_edge). If some edges are directed give to them the desired direction (make_directed). Suppose that the variable corresponding to the graph is named "ug".
- Perform the following sequence of steps:
plan_undi_graph pug(ug);
draw_undi_graph dug(pug,VISIBILITY);
The meaning of such steps is the following:
Constructor plan_undi_graph performs a "planarization" of the graph: an order is choosen for the edges around each node trying to keep the number of crossings between edges as low as possible. The name of the planarized graph so obtained is "pug". Variable "pug" is an object of the class plan_undi_graph.
Constructor draw_undi_graph constructs the final drawing by assigning each node with a position of the plane and each edge-segment with a length. Variable "dug" is an object of the class draw_undi_graph.
- At this point variable "dug" stores all the information that is needed to draw "ug" as an orthogonal drawing. For example, applying center to node "v" returns the coordinates of the center of "v".
Observe that if you have strict aesthetics requirements, you can replace
draw_undi_graph dug(pug, VISIBILITY);
with
draw_undi_graph dug(pug, VISIBILITY_COMPACTED);
in order to reduce the total edge-length of the drawing.
Note: the current version of GDT allows to apply option VISIBILITY only to graphs that are biconnected. A graph is biconnected if the removal of one node is not sufficient to cut it into two (or more) disconnected pieces.
An example of a visibilty representation drawn with GAPI is shown in the following figure:
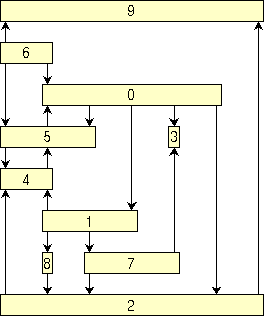
To draw directed graphs, GAPI offers an "upward-visibility" layout model. For more details, you can see the GAPI reference. An example of an upward-visibility drawing with a cross, is shown in the next figure:

Tree drawings
GDT currently provides two pre-defined tree layout algorithms: TreeCenterSons and TreeCenterSubtree. Please refer to the GAPI reference for further details.
|