title
Graph Drawing Toolkit

An object-oriented C++ library for handling and drawing graphs
Current Version: 4.0
Home
Project Description
Contact & Credits
Products
License
Supported platforms
Download
Documentation
Samples

Blag Tutorial

Orthogonal Drawings

Orthogonal drawings have an impressive range of applicability. In what follows we show how to use BLAG for constructing orthogonal drawings. First, we present a simple strategy, suitable for beginners (but still powerful enough to cover several applications). Second, we show how to work if performance is more important than aesthetics. Third, we describe how to behave if aesthetics are more important than performance. Fourth, we show how several choices are available for constructing drawings that moarere or less compact. Finally, we show how to customize the drawing according to your special requirements

A simple strategy

If you want to construct an orthogonal drawing of a graph with BLAG, simply do the following:

  • Construct the file "filename" containing your graph using the GDT file format.
  • Perform the commandline:
      blag filename conf
    Where "conf" is a configuration file that allows to customize the behaviour of BLAG. A full description of the cofiguration file syntax is given here. In this case we suggest the following content for "conf":

      <BOFF VERSION="1.1"/>
      <BEGIN_OPTIONS>
      <ALGORITHM> 1 </ALGORITHM>
      <END_OPTIONS>

    Algorithm number 1 corresponds to the default algorithm for orthogonal drawings.

  • At this point file "filename.exp" stores all the information that is needed to draw your graph as an orthogonal drawing, according to the simplified export format. Note that another file is also created, called "filename.gdt". It contains the same information in a format that is the internal format of GDT and that is a little more complicated.
An example of orthogonal drawing constructed with the previous steps is shown in the following figure.


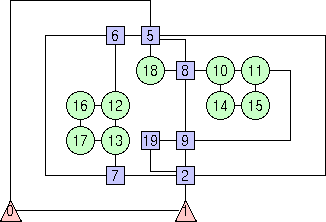
If performance is more important than aesthetics

If you have strict performance requirements, then you can change the configuration file shown above to obtain drawings that are slightly worse either in terms of number of bends along edges or in terms of global area occupied by the drawing. On the other hand you will have better time performance. GDT offers several facilities to explore the performance/effectiveness trade-off.

For example, if you accept to have more bends that those that are strictly needed, you can replace the above configuration file with the following one.

    <BOFF VERSION="1.1"/>
    <BEGIN_OPTIONS>
    <ALGORITHM> 0 </ALGORITHM>
    <END_OPTIONS>
This replaces the default algorithm for orthogonalization with a faster one.

Note: the current version of GDT allows to apply code 0 only to graphs that are biconnected and whose nodes have at most four incident edges. A graph is biconnected if the removal of one node is not sufficient to cut it into two (or more) disconnected pieces.

 

If aesthetics are more important than performance

If you have strict aesthetics requirements, you can replace the above configuration file with the following one.

    <BOFF VERSION="1.1"/>
    <BEGIN_OPTIONS>
    <ALGORITHM> 2 </ALGORITHM>
    <END_OPTIONS>
You will obtain drawings that are much better in terms of number of bends along edges. On the other hand you will have worse time performance. An orthogonal drawing constructed with code 2 of the same graph of the previous figure is shown below.

Note: the current version of GDT allows to apply code 2 only to graphs that are biconnected. A graph is biconnected if the removal of one node is not sufficient to cut it into two (or more) disconnected pieces.

Note: code 2 causes the invocation of a branch and bound algorithm, that is potentially exponential in time requirement. This makes it unsuitable for graphs with more that 100 vertices.


Drawing compaction

Several strategies are available for compacting orthogonal drawings. They have assigned an integer number in the interval 0 - 7. If no specification is given, then compaction 7 is applied as a default. If you want to force BLAG to use a certain compaction strategy, different from 7, you have to specify it as follows:

    <BOFF VERSION="1.1"/>
    <BEGIN_OPTIONS>
    <ALGORITHM> 1 </ALGORITHM>
    <COMPACTION> 3 </COMPACTION>
    <END_OPTIONS>
In this case BLAG will use the compaction strategy number 3. Usually, the best strategies, from the aesthetics point of view, are 2, 3, 6, and 7. On the other hand they are more time consuming than 0, 1, 4, and 5. Strategies 3 and 7 are strongly recommended for applications where having very compact drawings is a strict requirement.


Drawing customization

If you need to customize your drawing, then you can exploit the capability of GDT in handling user-specified constraints.

For example, if you want that all the nodes of a certain set (say 0, 5, and 6) are drawn in the same face (say with dummy label 1), then you can replace the above configuration file with the following one.

    <BOFF VERSION="1.1"/>
    <BEGIN_OPTIONS>
    <ALGORITHM> 1 </ALGORITHM>
    <CONSTRAINTS>
      <SAME_FACE_NODES>
        <NODE> 0 1
        <NODE> 5 1
        <NODE> 6 1
      </SAME_FACE_NODES>
    </CONSTRAINTS>
    <END_OPTIONS>
An example of orthogonal drawing constructed with a nodes 0, 5, and 6 on the same face is shown in the following figure.

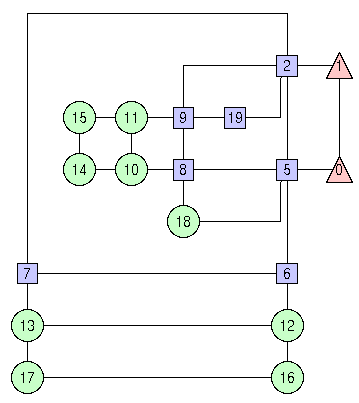
As another example, if you want to emphasize an edge (say edge 8) that for some reason is expecially important, then you might want to preserve it to have crossings and maybe to have bends. This is done very easily by replacing the above configuration file with the following one.

    <BOFF VERSION="1.1"/>
    <BEGIN_OPTIONS>
    <ALGORITHM> 1 </ALGORITHM>
    <CONSTRAINTS>
      <UNCROSSABLE_EDGES>
        <EDGE> 8
      </UNCROSSABLE_EDGES>
      <BENDS>
        <NONE>
          <EDGE> 8
        </NONE>
      </BENDS>
    </CONSTRAINTS>
    <END_OPTIONS>
A very useful feature of the new GDT release is the possibility of constraining each node of an orthogonal drawing to have a prescribed size. For example, consider the following graph:

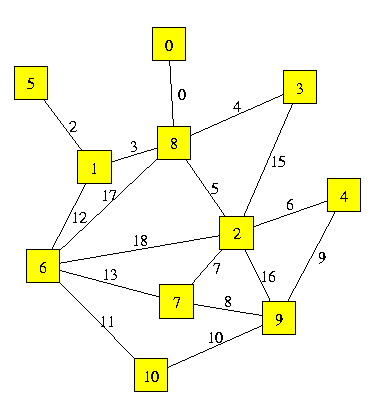
We can choose to draw it orthogonally, with the constraint that node 8 has width=1 and height=1, and node 2 has width=1 and height=3. The lengths are in terms of integer grid points. If not constrained, each node has width=height=0.

    <BOFF VERSION="1.1"/>
    <BEGIN_OPTIONS>
    <ALGORITHM> 1 </ALGORITHM>
    <CONSTRAINTS>
      <NODE_DIM NODE_ID="8" WIDTH="1" HEIGHT="1" />
      <NODE_DIM NODE_ID="2" WIDTH="1" HEIGHT="3" />
    </CONSTRAINTS>
    <END_OPTIONS>

 

top

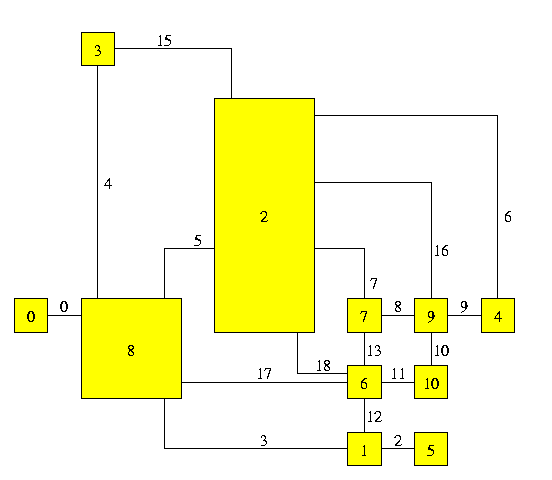
Polyline drawings

BLAG provides polyline layout algorithms. If you want to construct a polyline drawing of a graph with BLAG, simply do the following:
  • Construct the file "filename" containing your graph using the GDT file format.
  • Perform the commandline:
      blag filename conf
    Where "conf" is a configuration file that allows to customize the behaviour of BLAG. A full description of the cofiguration file syntax is given here. In this case we suggest the following content for "conf":
      <BEGIN_OPTIONS>
      <ALGORITHM> 7 </ALGORITHM>
      <END_OPTIONS>
    Algorithm number 7 corresponds to the default algorithm for polyline drawings.
  • At this point file "filename.exp" stores all the information that is needed to draw your graph as a visibility drawing, according to the simplified export format. Note that another file is also created, called "filename.gdt". It contains the same information in a format that is the internal format of GDT and that is a little more complicated.

Note: the current version of GDT allows to apply code 7 only to graphs that are biconnected. A graph is biconnected if the removal of one node is not sufficient to cut it into two (or more) disconnected pieces.

Examples of polyline drawings constructed with the previous steps are shown in the following figure.



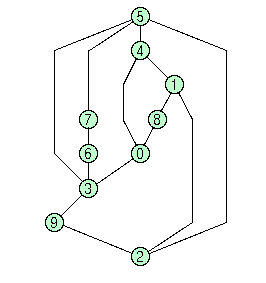
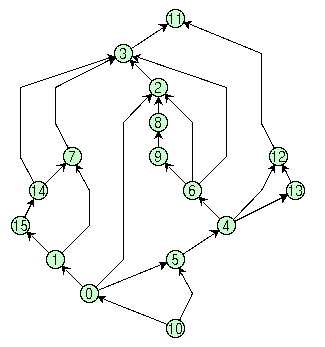
Several strategies are available for producing polyline drawings that are more or less compact. They have assigned an integer number in the interval 0 - 7. If no specification is given, then compaction 7 is applied as a default. If you want to force BLAG to use a certain compaction strategy, different from 7, you have to specify it as follows:

    <BEGIN_OPTIONS>
    <ALGORITHM> 7 </ALGORITHM>
    <COMPACTION> 3 </COMPACTION>
    <END_OPTIONS>
In this case BLAG will use the compaction strategy number 3. Usually, the best strategies, from the aesthetics point of view, are 2, 3, 6, and 7. On the other hand they are more time consuming than 0, 1, 4, and 5. Strategies 3 and 7 are strongly recommended for applications where having very compact drawings is a strict requirement.
top

Upward drawings

Upward drawings can be used in several applications, for example to draw Petri Nets or SADT diagrams. BLAG considers a more general model of upward drawing, in which some feedback edges are allowed when an upward drawing does not exist for the given graph. We call such a model "quasi-upward" drawing. In a quasi-upward drawing we call "bend" a point in which a feedback edge is tangent to the horizontal line through this point. In what follows we show how to use BLAG for constructing quasi-upward drawings.

First, we present a simple strategy, suitable for beginners (but still powerful enough to cover several applications). Second, we describe how to behave if aesthetics are more important than performance. Finally, we show how to customize the drawing according to your special requirements

A simple strategy

If you want to construct a quasi-upward drawing of a graph with BLAG, simply do the following:

  • Construct the file "filename" containing your graph using the GDT file format.
  • Perform the commandline:
      blag filename conf
    Where "conf" is a configuration file that allows to customize the behaviour of BLAG. A full description of the cofiguration file syntax is given here. In this case we suggest the following content for "conf":
      <BEGIN_OPTIONS>
      <ALGORITHM> 3 </ALGORITHM>
      <END_OPTIONS>
    Algorithm number 3 corresponds to the default algorithm for quasi-upward drawings.
  • At this point file "filename.exp" stores all the information that is needed to draw your graph as a quasi-upward drawing, according to the simplified export format. Note that another file is also created, called "filename.gdt". It contains the same information in a format that is the internal format of GDT and that is a little more complicated.
An example of quasi-upward drawing constructed with the previous steps is shown in the following figure. Observe that smoothed edges have been used to represent connections.

 

If aesthetics are more important than performance

If you have strict aesthetics requirements, you can replace the above configuration file with the following one.

    <BEGIN_OPTIONS>
    <ALGORITHM> 4 </ALGORITHM>
    <END_OPTIONS>
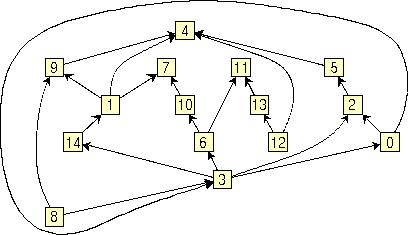
You will obtain drawings that are much better in terms of number of bends along edges. On the other hand you will have worse time performance. A quasi-upward drawing constructed with code 4 of the same graph of the previous figure is shown below.

 

Note: the current version of GDT allows to apply code 4 only to graphs that are biconnected. A graph is biconnected if the removal of one node is not sufficient to cut it into two (or more) disconnected pieces.

Note: code 2 causes the invocation of a branch and bound algorithm, that is potentially exponential in time requirement. This makes it unsuitable for graphs with more that 100 nodes.

Drawing customization

If you need to customize your drawing, then you can exploit the capability of GDT in handling user-specified constraints.

For example, if you want that all the nodes of a certain set (say 0, 5, and 6) are drawn in the same face (say with dummy label 1), then you can replace the above configuration file with the following one.

    <BEGIN_OPTIONS>
    <ALGORITHM> 3 </ALGORITHM>
    <CONSTRAINTS>
      <SAME_FACE_NODES>
        <NODE> 0 1
        <NODE> 5 1
        <NODE> 6 1
      </SAME_FACE_NODES>
    </CONSTRAINTS>
    <END_OPTIONS>
As another example, if you want to emphasize an edge (say edge 8) that for some reason is expecially important, then you might want to preserve it to have crossings and maybe to have bends. This is done very easily by replacing the above configuration file with the following one.
    <BEGIN_OPTIONS>
    <ALGORITHM> 3 </ALGORITHM>
    <CONSTRAINTS>
      <UNCROSSABLE_EDGES>
        <EDGE> 8
      </UNCROSSABLE_EDGES>
      <BENDS>
        <NONE>
          <EDGE> 8
        </NONE>
      </BENDS>
    </CONSTRAINTS>
    <END_OPTIONS>
top

Visibility drawings

BLAG provides several visibility layout algorithms. If you want to construct a visibility drawing of a graph with BLAG, simply do the following:
  • Construct the file "filename" containing your graph using the GDT file format.
  • Perform the commandline:
      blag filename conf
    Where "conf" is a configuration file that allows to customize the behaviour of BLAG. A full description of the cofiguration file syntax is given here. In this case we suggest the following content for "conf":
      <BEGIN_OPTIONS>
      <ALGORITHM> 8 </ALGORITHM>
      <END_OPTIONS>
    Algorithm number 8 corresponds to the default algorithm for standard visbility drawings.
  • At this point file "filename.exp" stores all the information that is needed to draw your graph as a visibility drawing, according to the simplified export format. Note that another file is also created, called "filename.gdt". It contains the same information in a format that is the internal format of GDT and that is a little more complicated.

Note: the current version of GDT allows to apply code 8 only to graphs that are biconnected. A graph is biconnected if the removal of one node is not sufficient to cut it into two (or more) disconnected pieces.

An example of visibility drawing constructed with the previous steps is shown in the following figure.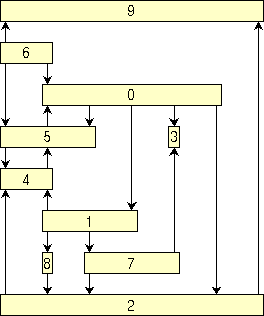



You can also apply an algorithm to draw directed graphs using "visibility-upward" layouts. Use for example the following file configuration:

    <BEGIN_OPTIONS>
    <ALGORITHM> 5 </ALGORITHM>
    <END_OPTIONS>
An example of "visibility-upward" drawing of a graph, produced with the above configuration file, is shown in the next figure:

Several strategies are available for producing visibility drawings that are more or less compact. They have assigned an integer number in the interval 0 - 7. If no specification is given, then compaction 7 is applied as a default. If you want to force BLAG to use a certain compaction strategy, different from 7, you have to specify it as follows:

    <BEGIN_OPTIONS>
    <ALGORITHM> 8 </ALGORITHM>
    <COMPACTION> 3 </COMPACTION>
    <END_OPTIONS>
In this case BLAG will use the compaction strategy number 3. Usually, the best strategies, from the aesthetics point of view, are 2, 3, 6, and 7. On the other hand they are more time consuming than 0, 1, 4, and 5. Strategies 3 and 7 are strongly recommended for applications where having very compact drawings is a strict requirement.
top

Tree drawings

In what follows we show how to use BLAG for constructing drawings of trees.

If you want to construct a tree drawing with BLAG, simply do the following:

  • Construct the file "filename" containing your tree using the GDT file format.
  • Perform the commandline:
      blag filename conf
    Where "conf" is a configuration file that allows to customize the behaviour of BLAG. A full description of the cofiguration file syntax is given here. In this case we suggest the following content for "conf":
      <BEGIN_OPTIONS>
      <ALGORITHM> 9 </ALGORITHM>
      <END_OPTIONS>
    Number 9 corresponds to the TreeCenterSons algorithm. Alternatively, you can use number 10, that is TreeCenterSubtree.
  • At this point file "filename.exp" stores all the information that is needed to draw your tree, according to the simplified export format. Note that another file is also created, called "filename.gdt". It contains the same information in a format that is the internal format of GDT and that is a little more complicated.
An example of tree constructed with the previous steps is shown in the following figure.

tree
top

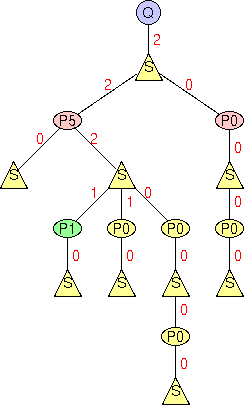
Last update: February 08, 2008