
CAPITOLO 3 " STABILIZZAZIONE E PSEUDO-STABILIZZAZIONE "
Introduzione Un semplice esempio di protocollo Pseudo-stabilizzante
I sistemi auto-stabilizzanti sono estremamente robusti sotto l'aspetto di errori; questo spiega il notevole interesse per essi.
Lo scopo di questo capitolo è quello di "investigare" i criteri per il "buon comportamento" dei sistemi, quando per essi si ha una inizializzazione arbitraria.
Il primo criterio per la nozione di "buon comportamento", malgrado l'inizializzazione arbitraria può essere fatto risalire agli scritti originari di Dijkstra sull’auto-stabilizzazione.
Tale criterio richiede che un sistema, partendo da uno stato arbitrario, garantisce il raggiungimento, entro un numero finito di transizioni, di uno stato dopo il quale il sistema non devia dalle sue specifiche iniziali. I sistemi che soddisfano questo criterio vengono chiamati pseudo-stabilizzanti.
Viceversa il concetto di stabilizzazione, inizialmente descritto da Dijkstra, già citato nel capitolo 1 e che qui richiamiamo, richiede che se un sistema parte da uno stato arbitrario, allora esso garantisce il raggiungimento, entro un numero finito di transizioni, di uno stato dopo il quale il sistema non può deviare dalle specifiche iniziali.
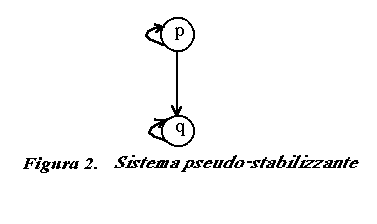
La fragile distinzione tra stabilizzazione e pseudo-stabilizzazione è meglio illustrata con un esempio. Consideriamo un sistema con un diagramma delle transizioni di stato come mostrato in figura 1 (In questo diagramma i cerchi rappresentano gli stati del sistema e gli archi rappresentano le transizioni fra gli stati).
Partendo da un qualsiasi stato di questo sistema è garantito il raggiungimento, entro una transizione, o nello stato p o nella stato q.
Da p può essere eseguita solo una computazione (p,p,..) così come da q (cioè (q,q,…)).
Così, se la specifica iniziale di questo sistema è F={(p,p,..),(q,q,..)} allora il sistema raggiungerà, con una transizione, uno stato (p o q) dal quale deviare da F è impossibile. Dunque il sistema è stabilizzante.

Ora, consideriamo un secondo sistema con un diagramma delle transizioni di stato come mostrato in figura 2, e assumiamo che la specifica iniziale di questo sistema sia come prima F. Questo sistema è non stabilizzante perché partendo dallo stato p non è garantito che il sistema lascerà mai p. Infatti il sistema può deviare da F eseguendo la computazione (p,q,q,...) che non è presente in F. D'altra parte ogni computazione di questo sistema è in una delle seguenti forme :
(p,p...) ; (p,..p,q,q,...) ; (q,q,...)
Pertanto ogni computazione ha suffissi infiniti in F.
In altre parole, durante ogni computazione il sistema garantisce il raggiungimento di uno stato dopo il quale il sistema non devia da F, sebbene esso possa avere un numero infinito di scelte da fare. Dunque il sistema è pseudo-stabilizzante.
Come verrà mostrato successivamente la pseudo-stabilizzazione è effettivamente più fragile della stabilizzazione con "non devia" al posto di "non può deviare"; pertanto ogni sistema stabilizzante è anche pseudo-stabilizzante ma non è vero il viceversa, cioè ci sono dei sistemi pseudo-stabilizzanti che non sono stabilizzanti.
Molti progettisti di sistema sostengono tuttavia che i sistemi pseudo-stabilizzanti sono più adeguati per gli scopi pratici e non c'è una reale necessità di trasformare tali sistemi in sistemi stabilizzanti, soprattutto se il prezzo della stabilizzazione è molto alto.
3.2 ATTRACTORS E PSEUDO-ATTRACTORS
In questo paragrafo definiamo dei sistemi e la loro regione di esecuzione e identifichiamo due tipi di regioni chiamate "attractors" e "pseudo-attractors".
Supponiamo che S sia un sistema definito da un insieme di stati e da un insieme di transizioni, dove ogni transizione è una coppia ordinata di stati.
Una regione del sistema S è un sottoinsieme degli stati del sistema.
Una regione P è CHIUSA se e solo se per ogni stato p e q , se p è in P e (p,q) è una transizione allora q è in P.
Una COMPUTAZIONE di S è una non vuota sequenza massimale (p1,p2,...), dove ogni pi è uno stato del sistema e ogni (pi,pi+1) è una transizione del sistema.
Una computazione CONDUCE in una regione P se e solo se essa ha uno stato in P.
DEFINIZIONE 1 : Una regione P di S è una ATTRACTORS se e solo se essa soddisfa le seguenti due condizioni :
a) P è chiusa;
b) Ogni computazione di S conduce a P.
Inoltre una volta che una computazione raggiunge una attractors, essa rimarrà lì indefinitamente.
DEFINIZIONE 2 : Una sequenza infinita (P1,P2,...) di regioni di S è una PSEUDO-ATTRACTORS se e solo se essa soddisfa le due seguenti condizioni :
a) Per ogni k, con k=1,2,.., la regione
è chiusa;
b) Ogni computazione di S conduce alla regione
.
Supponiamo (P1,P2,...) essere una pseudo-attractors di qualche sistema, per ogni computazione del sistema, c'è un k, con k=1,2,.. tale che la computazione raggiungerà alla fine una regione Pk ma non raggiungerà mai nessuna delle precedenti regioni P1,..,Pk-1. In questo caso la computazione rimarrà in Pk indefinitamente
( allora ![]() è chiusa ).
è chiusa ).
Il prossimo teorema, che segue direttamente dalla precedente definizione, fornisce una interessante relazione tra attractors e pseudo-attractors.
TEOREMA 1 : Supponiamo P essere una regione di S e (P1,P2,...) essere una sequenza infinita di regioni di S.
a) se P è una attractor di S allora (P,P,..) è una pseudo-attractors di S;
b) se (P1,P2,...) è una pseudo-attractors di S allora la
è una attractors di S.
3.3 STABILIZZAZIONE E PSEUDO-STABILIZZAZIONE
Una SPECIFICA di un sistema S è un insieme di computazioni di S. Successivamente verificheremo che ciò abbia senso per un sistema sia che sia stabilizzante sia che sia pseudo-stabilizzante per una data specifica; ma prima adottiamo le seguenti notazioni :
NOTAZIONI : Supponiamo c essere qualche computazione che ha almeno i stati.
Allora c.i denota l'iesimo stato in c, e c i denota che il suffisso di c
inizia con l'iesimo stato c.i.
DEFINIZIONE 3 : Un sistema S si stabilizza verso una specifica F se e solo se per
ogni computazione c di S, $ un intero positivo i tale che ogni com_
putazione di S che inizia con lo stato c.i è in F.
DEFINIZIONE 4 : Un sistema S si pseudo-stabilizza verso una specifi ca F se e solo se
per ogni computazione c di S, $ un intero positivo i tale che la computazione c i è in F.
Informalmente, il sistema S si stabilizza verso una specifica F se e solo se, partendo da uno stato arbitrario, S garantisce il raggiungimento in uno stato dopo il quale F non può essere violata. Al contrario, S si pseudo-stabilizza verso F se e solo se partendo da uno stato arbitrario, S garantisce il raggiungimento in uno stato dopo il quale F non è violata.
Così la distinzione tra le due definizioni si riduce alla differenza tra "non può" e "non è". Questa distinzione non può essere individuata da un osservatore esterno al sistema, egli può solamente osservare :
(1) la computazione che il sistema esegue;
(2) che la specifica iniziale non è violata dopo alcuni passi nella computazione.
Lo stesso osservatore non riesce ad osservare che la specifica iniziale non può essere violata dopo alcuni passi. In altre parole, un osservatore esterno può osservare la pseudo-stabilizzazione ma non la stabilizzazione ( perché egli deve essere all'interno per poterla osservare) .
Questo suggerisce che la stabilizzazione e la pseudo-stabilizzazione sono indistinguibili per tutti gli scopi pratici, anche se i due concetti sono distinti. In particolare, la stabilizzazione è una proprietà più stringente della pseudo-stabilizzazione come mostrato dal seguente teorema.
TEOREMA 2 : Ogni sistema che si stabilizza verso qualche specifica F si pseudo-stabilizza verso la stessa F, l’inverso non è necessariamente vero.
Consideriamo un sistema S dove gli stati sono {p,q} e le transizioni sono {(p,p),(p,q),(q,q)} e il cui diagramma delle transizioni di stato sia quello mostrato in figura 2 a pag. 8 nel paragrafo 3.1. F è una possibile specifica di S e consiste in due infinite computazioni : F={(p,p,..),(q,q,..)}
Il sistema S non si stabilizza verso F perché l’infinita computazione (p,p,..) di S non ha stato, tanto che ogni computazione che inizia da quello stato è in F. D'altro lato S si pseudo-stabilizza verso F perché ciascuna computazione di S è in una delle seguenti forme :
(p,p,..) ; (p,p,..,p,q,q,..) oppure (q,q,...)
Così ogni computazione di S ha un suffisso in F.
Il prossimo teorema mostra che la stabilizzazione ha un vantaggio al di sopra della pseudo-stabilizzazione in sistemi con un numero finito di stati.
TEOREMA 3 : Supponiamo S essere un sistema con n stati, e supponiamo F essere una specifica di S.
a) se S si stabilizza verso F, allora per ogni computazione c, $ un intero positivo k tale che k £ n+1 e c k è in F;
b) se S semplicemente si pseudo-stabilizza verso F non necessariamente si ha la precedente conclusione (cioè il punto a).
3.4 RELAZIONE TRA ATTRACTION E STABILIZZAZIONE
In questo paragrafo vengono presentati due teoremi che sono delle condizioni sufficienti per stabilire che un dato sistema S si stabilizza o si pseudo-stabilizza verso una data specifica F. In particolare verrà mostrato che se S ha una (pseudo-) attractor che, soddisfacendo certe condizioni, include F allora S si pseudo-stabilizza verso F.
Un esempio di applicazione di questo metodo per stabilire che un dato sistema si pseudo-stabilizza verso una sua specifica è discusso nel prossimo paragrafo.
TEOREMA 4 : Supponiamo S essere un sistema con una specifica F.
Se S ha una attractor P, tanto che ogni computazione di S a gli stati tutti in P e in F, allora S si stabilizza verso F.
TEOREMA 5 : Supponiamo S essere un sistema con una specifica F. Se S ha una pseudo-attractor (P1,P2,..) così che ogni computazione di S i cui stati sono tutti nello stesso Pi, con i=1,2,.., ha un suffisso in F, allora S si stabilizza verso F.
3.5 UN SEMPLICE ESEMPIO DI PROTOCOLLO PSEUDO-STABILIZZANTE
Nei prossimi paragrafi verrà presentato, dapprima in maniera informale e successivamente in maniera formale, un semplice esempio di protocollo pseudo-stabilizzante il " protocollo di alternating-bit ".
3.5.1 PRESENTAZIONE INFORMALE DEL PROTOCOLLO DI ALTERNATING-BIT
Nella presentazione del protocollo faremo riferimento ad un sistema di due processi. Il termine " sistema " è inteso in senso generale, cioè può rappresentare una rete di workstation che comunicano tra loro oppure può rappresentare una singola macchina sulla quale si ha una comunicazione client-server.
Consideriamo pertanto un sistema di due processi s e r che comunicano scambiandosi messaggi attraverso due canali. Ogni canale è un unbounded FIFO buffer (cioè un buffer illimitato gestito con una politica First-In-First-Out) che immagazzina i messaggi spediti da un processo finche` ciascuno di loro è ricevuto dall'altro processo oppure finche` viene perduto per esempio scomparendo dal canale.

Il protocollo adottato è il seguente :
a) Il processo s spedisce un data message alla volta. Dopo aver spedito ciascun
b) Se dopo aver spedito un data message il processo s non riceve un messaggio di
In questo caso il processo s dopo un certo time out rispedisce l'ultimo data message.
c) Ogni data message ha due settori : data(t,b)
Se successivamente s rispedisce il data message, il messaggio rispedito avrà lo stesso b (e lo stesso t) come l'ultimo messaggio.
3.5.2 PRESENTAZIONE FORMALE DEL PROTOCOLLO
Il programma di ciascuno dei due processi s e r è un insieme di azioni che hanno la forma : begin<azione> |....| <azione>end
Il simbolo | è un separatore che separa le differenti azioni dei processi nel programma. Ogni azione ha la sintassi :
<guardia> ® <sequenza di istruzioni>
Ogni guardia è in una delle seguenti forme :
<guardia locale>,
rcv<messaggio>, oppure
timeout<guardia globale>
Dove la "guardia locale" è una espressione booleana attraverso delle variabili locali del suo processo, e la "guardia globale" è una espressione booleana attraverso le variabili dei due processi s e r, e il contenuto dei due canali. Il contenuto di un canale è una sequenza di messaggi.
Spedire un messaggio consiste nel metterlo in coda alla sequenza di messaggi, mentre ricevere un messaggio consiste nel rimuoverlo dalla testa della sequenza.
Il contenuto del canale a, denotato con Csr, è una sequenza di data message. Il contenuto del canale b, denotato con Crs, è una sequenza di messaggi di ack.
Il programma per il processo s è il seguente :
process s
const in: array[integer] of text /* testo di tutti i messaggi da spedire */
var ns:integer init 0 /* indice dell'array "in" */
readys:boolean init true /* pronto ha spedire il successivo data message.*/
bs:(0,1) init 0 /* alternating-bit */
begin readys ® readys:=false; send data(in[ns],bs)
| rev ack ® ns,readys,bs:=ns=1, true, 1-bs
| timeout ( Ø (readys) Ù Ø (readyr) Ù (Csr=<>) Ù (Crs=<>) )
® send data(in[ns],bs)
end s
Il processo s ha tre azioni. Nella prima azione s spedisce il primo data message ad r ed aspetta un messaggio di ack. Nella seconda azione, s riceve un messaggio di ack (presumibilmente per l'ultimo data message che egli ha spedito) e diventa pronto per spedire il successivo data message.
Nella terza azione quando nessuno dei due processi può spedire (messaggi) e i due canali sono vuoti (indicando così una perdita di messaggi), il processo s dopo un time out rispedisce l'ultimo data message.
Il programma per il processo r è il seguente :
process r
const out: array[integer] of text /* testo di tutti i messaggi ricevuti */
var nr:integer /* indice dell'array "out" */
readyr:boolean init false /* pronto ha replicare con un ack */
br:(0,1) init 0 /* alternating-bit aspettato */
t:text /* testo ricevuto */
b:(0,1) /* alternating-bit ricevuto */
begin rcv data(t,b) ® if b=br then out[nr],nr,br:=t,nr+1,1-br fi;
readyr:=true
|readyr ® readyr:=false; send ack
end r
Il processo r ha due azioni. Nella prima azione, r riceve un data message e verifica se è un messaggio originale che deve essere immagazzinato o se esso è la ripetizione dell' ultimo messaggio ricevuto e che quindi potrebbe essere abbandonato. Nel caso in cui il messaggio ricevuto è un originale, r diventa pronto per replicare con un messaggio di ack il quale è spedito nella seconda azione di r.
3.5.3 SPECIFICA DEL PROTOCOLLO
Uno stato del protocollo è definito da un valore per ogni variabile dei due
processi, e da una sequenza di data message per il canale a, e da una sequenza di
messaggi di ack per il canale b.
Un’azione di uno dei due processi è permessa in un dato stato, se e solo se la guardia di ciascuno dei due processi è un locale ,o globale ,predicato il cui valore è vero per un dato stato, oppure se la sua guardia è della forma rcv<messaggio> e il canale di input del suo processo ha almeno un messaggio (a un dato stato).
Uno stato q del protocollo segue da uno stato p se e solo se almeno una azione, di uno dei due processi, è permessa a p che eseguendo la sequenza di istruzioni dell’azione "permessa" iniziando da p produce q.
Una computazione del protocollo è una infinita sequenza di stati del protocollo: p1,p2,.. tale che ogni pi+1 segue a pi. (notare che il protocollo non ha stati terminali; così tutte le sue computazioni sono infinite).
Supponiamo che p sia uno stato del protocollo. Per comodità supponiamo in,ns,out, e nr denotati rispettivamente dal valore delle variabili in,ns,out, e nr. Supponiamo anche ms e mr essere due interi. Lo stato p è (ms,mr)-safe se e solo se contiene le seguenti condizioni :
(ms£ ns) Ù (mr£ nr) Ù (" i tale che 0£ i< nr-mr : in[ms+i]=out[mr+i])
Una computazione del protocollo è "ben riuscita", cioè ha esito positivo, se e solo se la variabile nr è incrementata spesso, ed infinitamente, lungo la computazione e ci sono due interi ms e mr tali che ogni stato nella computazione è (ms,mr)-safe.
Il protocollo è specificato da un insieme F di tutte le computazioni che hanno successo.
3.5.4 PSEUDO-STABILIZZAZIONE DEL PROTOCOLLO
Consideriamo un sistema costituito da due processi s ed r, e una azione di "messaggio perduto" la quale quando eseguita abbandona un messaggio (al limite da uno dei due canali tra s e r). Assumiamo che lungo ciascuna (infinita) computazione del sistema, se qualche messaggio è spedito ripetutamente da un processo allora esso è eventualmente ricevuto dall'altro processo.
In questo paragrafo verrà mostrato che il sistema ha una pseudo-attractor (P1,P2,..) tale che ogni computazione del sistema, i cui stati sono tutti nella stessa Pi , con i=1,2,.., ha un suffisso in F.
Definiamo una funzione "rank" che assegna ad ogni stato p del sistema un numero naturale rank.p come di seguito :
rank.p = Il numero di data message nel canale a + il numero dei messaggi di ack nel canale b + X.p +Y.p
Dove :
X.p=0 se readys=false allo stato p, 1 altrimenti. e
Y.p=0 se readyr=false allo stato p, 1 altrimenti.
Notare che ciascuna azione nei due processi del protocollo riduce il valore di rank partendo da 1 o lo mantiene invariato. Il messaggio di "azione perduta" riduce il valore di rank partendo da 1.
Consideriamo una sequenza infinita (P1,P2,..), in cui
P1=[p: p è uno stato del sistema in cui rank.p=0 o rank.p=1],
e per i=2,3,... è Pi=[p: p è uno stato del sistema in cui rank.p=i]
È facile mostrare che (P1,P2,..) è una pseudo-attractor del sistema.
Primo, ogni azione nel sistema, oltre che l’azione di time out, riduce il valore di rank o lo mantiene invariato.
L’azione di time out
incrementa il valore di rank da 0 a 1 ma tuttavia (ancora)
mantiene gli stati del sistema dentro Pi. Dunque, la
regione ![]() è chiusa
per ogni k, con k=1,2, .
è chiusa
per ogni k, con k=1,2, .
Secondo, dal momento che il valore di rank.p è un numero naturale per ogni stato del sistema p, ogni stato del sistema è nello stesso Pi .
Dunque, ogni computazione
del sistema conduce nella regione ![]() .
.
Questo completa la dimostrazione che (P1,P2,..) è una pseudo-attractor del sistema.
Rimane ora da mostrare che ogni computazione del sistema, i cui stati sono tutti nel medesimo Pi, con i=1,2,.., ha un suffisso in F.
Consideriamo una computazione i cui stati sono tutti nello stesso Pi, di seguito vengono discussi i due casi di i=1 e i> 1 separatamente.
Se i=1, allora ad ogni stato della computazione c’è al massimo un messaggio nei due canali tra s ed r, è facile mostrare che tale computazione ha un suffisso in F (prevedendo che ogni messaggio che è spedito è alla fine sempre ricevuto).
Se i>1 allora ogni stato nella computazione ha lo stesso rank i questo significa che l’azione di "messaggio perduto" non è mai eseguita (perché essa riduce il rank). Inoltre l’azione di time out nel processo s non è mai permessa, e così mai eseguita. Lungo la computazione , il processo s attende di ricevere un messaggio di ack allora spedisce il successivo data message (con un valore del bit differente dall’ultimo data message), e il processo r mantiene il sopra ricevuto data message con l’aspettato alternating-bit immagazzinandolo nell’array out, successivamente spedirà indietro un messaggio di ack.