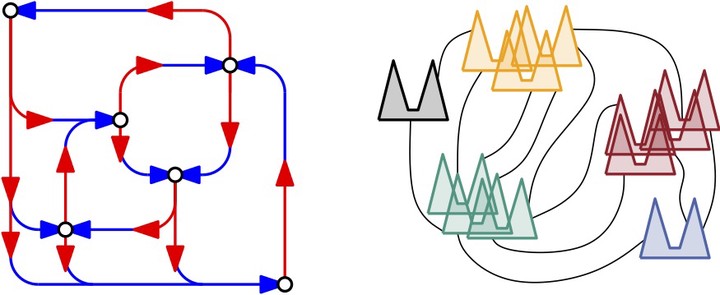
 (left) A planar L-drawing of a directed graph. (right) A planar intersection-link representation of a flat clustered graph with clusters containing at most $2$ vertices, using $2$-combs as geometric objects. Both representations are associated with $4$-modal embeddings
(left) A planar L-drawing of a directed graph. (right) A planar intersection-link representation of a flat clustered graph with clusters containing at most $2$ vertices, using $2$-combs as geometric objects. Both representations are associated with $4$-modal embeddings
Abstract
Given a planar digraph $G$ and a positive even integer $k$, an embedding of $G$ in the plane is $k$-modal, if every vertex of $G$ is incident to at most $k$ pairs of consecutive edges with opposite orientations, i.e., the incoming and the outgoing edges at each vertex are grouped by the embedding into at most $k$ sets of consecutive edges with the same orientation. In this paper, we study the $k$-Modality problem, which asks for the existence of a $k$-modal embedding of a planar digraph. This combinatorial problem is at the very core of a variety of constrained embedding questions for planar digraphs and flat clustered networks.
First, since the $2$-Modality problem can be easily solved in linear time, we consider the general $k$-Modality problem for any value of $k>2$ and show that the problem is NP-complete for planar digraphs of maximum degree $\Delta \geq k+3$. We relate its computational complexity to that of two notions of planarity for flat clustered networks$:$ Planar Intersection-Link and Planar NodeTrix representations. This allows us to answer in the strongest possible way an open question by Di Giacomo et al. GD17, concerning the complexity of constructing planar NodeTrix representations of flat clustered networks with small clusters, and to address a research question by Angelini et al. JGAA17, concerning intersection-link representations based on geometric objects that determine complex arrangements. On the positive side, we provide a simple FPT algorithm for partial $2$-trees of arbitrary degree, whose running time is exponential in $k$ and linear in the input size.
Second, motivated by the recently-introduced planar L-drawings of planar digraphs GD17, which require the computation of a $4$-modal embedding, we focus our attention on $k=4$. On the algorithmic side, we show a complexity dichotomy for the $4$-Modality problem with respect to $\Delta$, by providing a linear-time algorithm for planar digraphs with $\Delta \leq 6$. This algorithmic result is based on decomposing the input digraph into its blocks via BC-trees and each of these blocks into its triconnected components via SPQR-trees. In particular, we are able to show that the constraints imposed on the embedding by the rigid triconnected components can be tackled by means of a small set of reduction rules and discover that the algorithmic core of the problem lies in special instances of NaeSat, which we prove to be always NAE-satisfiable–a result of independent interest that improves on Porschen et al. SAT03.
Finally, on the combinatorial side, we consider outerplanar digraphs and show that any such a digraph always admits a $k$-modal embedding with $k=4$ and that this value of $k$ is best possible for the digraphs in this family.