L-Drawings of Directed Graphs
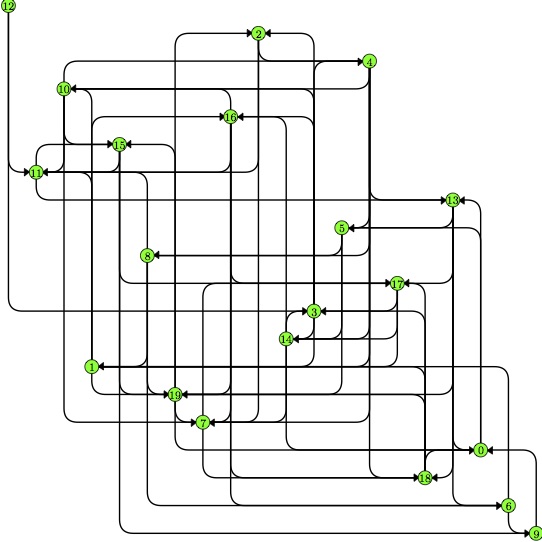 An L-drawing of a random graph
An L-drawing of a random graph with $20$ vertices and $76$ edges
Abstract
We introduce L-drawings, a novel paradigm for representing directed graphs aiming at combining the readability features of orthogonal drawings with the expressive power of matrix representations. In an L-drawing, vertices have exclusive $x$- and $y$-coordinates and edges consist of two segments, one exiting the source vertically and one entering the destination horizontally.
We study the problem of computing L-drawings using minimum ink. We prove its NP-completeness and provide a heuristics based on a polynomial-time algorithm that adds a vertex to a drawing using the minimum additional ink. We performed an experimental analysis of the heuristics which confirms its effectiveness.
Type
Publication
In 42nd International Conference on Current Trends in Theory and Practice of Computer Science (SOFSEM 2016)