On Some NP-complete SEFE Problems
 A shift ring consisting of several flow switches. The red arrows illustrate the flow of information
A shift ring consisting of several flow switches. The red arrows illustrate the flow of information
Abstract
In this work we investigate the complexity of some combinatorial problems related to the Simultaneous Embedding with Fixed Edges (SEFE) and the PARTITIONED T-COHERENT $k$-PAGE BOOK EMBEDDING (PTBE-$k$) problems, which are known to be equivalent under certain conditions.
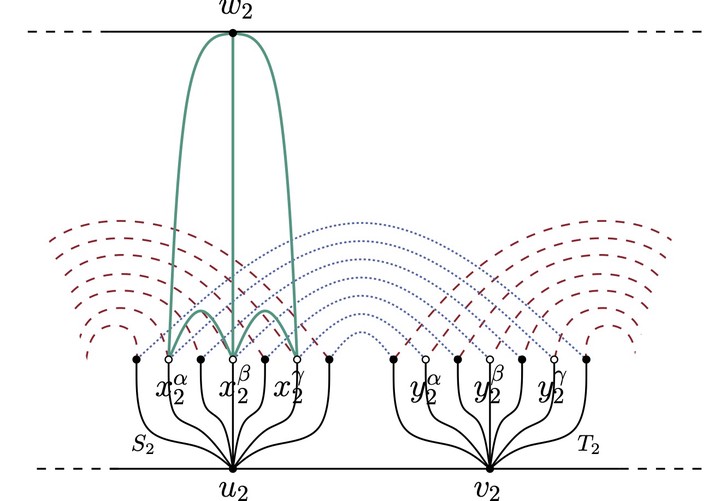
Given $k$ planar graphs on the same set of $n$ vertices, the SEFE problem asks to find a drawing of each graph on the same set of $n$ points in such a way that each edge that is common to more than one graph is represented by the same curve in the drawings of all such graphs.
Given a tree $T$ with $n$ leaves and a collection of $k$ edge-sets $E_i$ connecting pairs of leaves of $T$, the PTBE-$k$ problem asks to find an ordering $\mathcal{O}$ of the leaves of $T$ that is represented by $T$ such that the endvertices of two edges in any set $E_i$ do not alternate in $\mathcal{O}$.
The SEFE problem is $\mathcal{NP}$-complete for $k \geq 3$ even if the intersection graph is the same for each pair of graphs (sunflower intersection). We prove that this is true even when the intersection graph is a tree and all the input graphs are biconnected. This result implies the $\mathcal{NP}$-completeness of PTBE-$k$ for $k\geq 3$. However, we prove stronger results on this problem, namely that PTBE-$k$ remains $\mathcal{NP}$-complete for $k\geq 3$ even if (i) two of the input graphs $G_i = T \cup E_i $ are biconnected and $T$ is a caterpillar or if (ii) $T$ is a star. This latter setting is also known in the literature as PARTITIONED $k$-PAGE BOOK EMBEDDING. On the positive side, we provide a linear-time algorithm for PTBE-$k$ when all but one of the edge-sets induce connected graphs.
Finally, we prove that the problem of maximizing the number of edges that are drawn the same in a SEFE of two graphs (optimization of SEFE) is $\mathcal{NP}$-complete, even in several restricted settings.