Planar Embeddings with Small and Uniform Faces
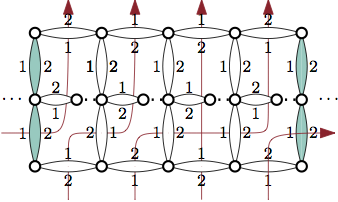 A shift ring consisting of several flow switches. The red arrows illustrate the flow of information
A shift ring consisting of several flow switches. The red arrows illustrate the flow of information
Abstract
Motivated by finding planar embeddings that lead to drawings with favorable aesthetics, we study the problems MINMAXFACE and UNIFORMFACES of embedding a given biconnected multi-graph such that the largest face is as small as possible and such that all faces have the same size, respectively.
We prove a complexity dichotomy for MINMAXFACE and show that deciding whether the maximum is at most $k$ is polynomial-time solvable for $k \leq 4$ and $\mathcal{NP}$-complete for $k \geq 5$. Further, we give a $6$-approximation for minimizing the maximum face in a planar embedding. For UNIFORMFACES, we show that the problem is $\mathcal{NP}$-complete for odd $k \geq 7$ and even $k \geq 10$. Moreover, we characterize the biconnected planar multi-graphs admitting $3$- and $4$-uniform embeddings (in a $k$-uniform embedding all faces have size $k$) and give an efficient algorithm for testing the existence of a $6$-uniform embedding.