Morphing Planar Graph Drawings Optimally
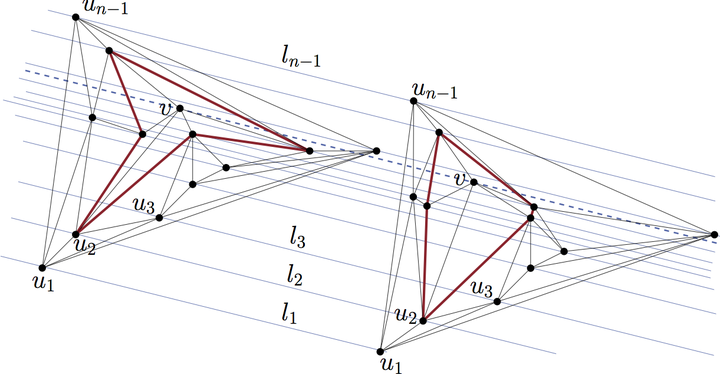 Illustration of the “Fast Convexifier” procedure
Illustration of the “Fast Convexifier” procedure
Abstract
We provide an algorithm for computing a planar morph between any two planar straight-line drawings of any $n$-vertex plane graph in $O(n)$ morphing steps, thus improving upon the previously best known $O(n^2)$ upper bound. Further, we prove that our algorithm is optimal, that is, we show that there exist two planar straight-line drawings $\Gamma_s$ and $\Gamma_t$ of an $n$-vertex plane graph $G$ such that any planar morph between $\Gamma_s$ and $\Gamma_t$ requires $\Omega(n)$ morphing steps.
Type
Publication
In 41st International Colloquium on Automata, Languages, and Programming (ICALP 2014)