Strip Planarity Testing
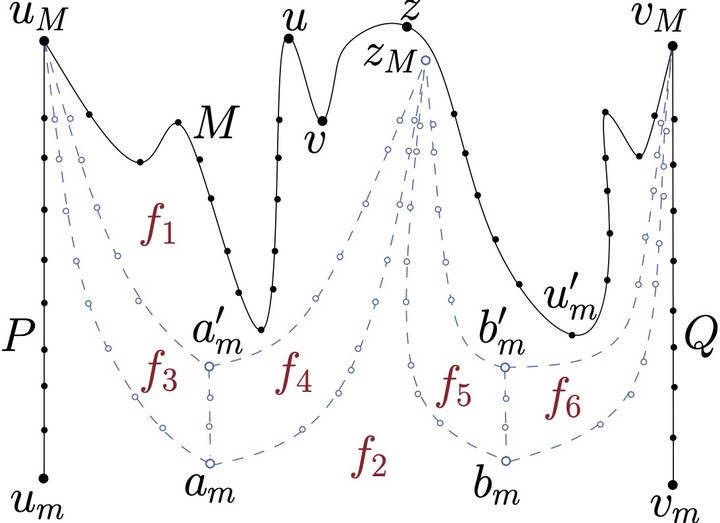 Augmentation of $(G, \gamma)$ inside a face $f$
Augmentation of $(G, \gamma)$ inside a face $f$
Abstract
In this paper we introduce and study the strip planarity testing problem, which takes as an input a planar graph $G(V,E)$ and a function $\gamma:V \rightarrow {1,2,\dots,k}$ and asks whether a planar drawing of $G$ exists such that each edge is monotone in the $y$-direction and, for any $u,v\in V$ with $\gamma(u)<\gamma(v)$, it holds $y(u) < y(v)$. The problem has strong relationships with some of the most deeply studied variants of the planarity testing problem, such as clustered planarity, upward planarity, and level planarity. We show that the problem is polynomial-time solvable if $G$ has a fixed planar embedding.
Type
Publication
In 21nd International Symposium on Graph Drawing and Network Visualization (GD 2013)